État quantique - Définition

En mécanique quantique, l'état d'un système décrit tous les aspects du système physique. Il est représenté par un objet mathématique qui donne le maximum d'information possible sur le système, dans le but de prévoir les résultats des expériences que l'on peut réaliser. Une différence fondamentale entre la mécanique classique et la mécanique quantique tient à la façon dont est décrit l'état d'un système physique. On a coutume de dire qu'un système quantique peut être dans plusieurs états à la fois.

La notion d'état en mécanique classique

En mécanique classique, le système le plus élémentaire est un point matériel de masse m. L'état de ce système est complètement décrit par la donnée du vecteur position et de la quantité de mouvement du point matériel. Autrement dit, l'état du système est repéré par un point dans un espace vectoriel de dimension 6 (3 pour le vecteur position et 3 pour le vecteur vitesse). Si l'on connait l'état du système à un instant donné, ainsi que les forces qui agissent sur lui par la suite, l'équation fondamentale de la dynamique nous permet de calculer l'état du système à un instant ultérieur.

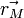
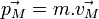
L'espace des états dépend du système considéré : si l'on considère non plus un mais N points matériels, l'état du système sera repéré par un point dans un espace vectoriel de dimension 6N, car il faut garder la trace de la position et de l'impulsion de chacun des N points matériels ; et dans le cas d'un milieu continu, comme un fluide ou un solide déformable, l'état du système est décrit par un champ de déformation, un champ de densité massique et un champ de vecteurs vitesse. Là encore, l'état d'un système à l'instant t + τ peut se déduire de l'état du système à l'instant t.

La notion d'état en mécanique quantique - état et mesure

Pour un système quantique, il est nécessaire de distinguer les grandeurs physiques observables de l'état du système proprement dit. En mécanique classique, cette différence n'existe pas : et représentent aussi bien l'état du système que les grandeurs physiques position et impulsion. Ainsi, si l'on veut connaître l'état d'un système classique, il suffit de mesurer les deux grandeurs physiques impulsion et position, et l'état est totalement déterminé. Pour un système plus complexe qu'un point matériel, le nombre de grandeurs à mesurer est plus important, mais il est en principe toujours possible de déterminer l'état du système. À l'inverse, en mécanique quantique, l'état d'un système physique n'est en général jamais totalement mesurable.

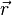
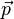
Considérons par exemple le système quantique le plus simple possible, c’est-à-dire une particule sans spin. Ce système est très similaire au point matériel de la mécanique classique. En effet les grandeurs physiques observables, ou plus simplement les observables sont les mêmes dans les deux cas : la position, l'impulsion, l'énergie cinétique, l'énergie potentielle, l'énergie totale,… Supposons que notre particule soit préparée dans un état i que l'on souhaite déterminer. On peut concevoir une expérience permettant de déterminer la position, par exemple en éclairant la particule, qui donnera comme résultat : 'la particule est en '. On pourrait alors en conclure que la position d'une particule préparée dans l'état i est . Cependant, si l'on réitère l'expérience sur la même particule à nouveau préparée dans l'état i, nous obtiendrons une autre position  ! Il en serait de même avec toute autre grandeur observable.

Histogramme : statistique des résultats de N=5000 mesures de la position d'un ensemble de particules toutes préparées dans le même état. Courbe : densité de probabilité de présence mise à la même échelle.

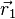
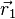
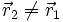
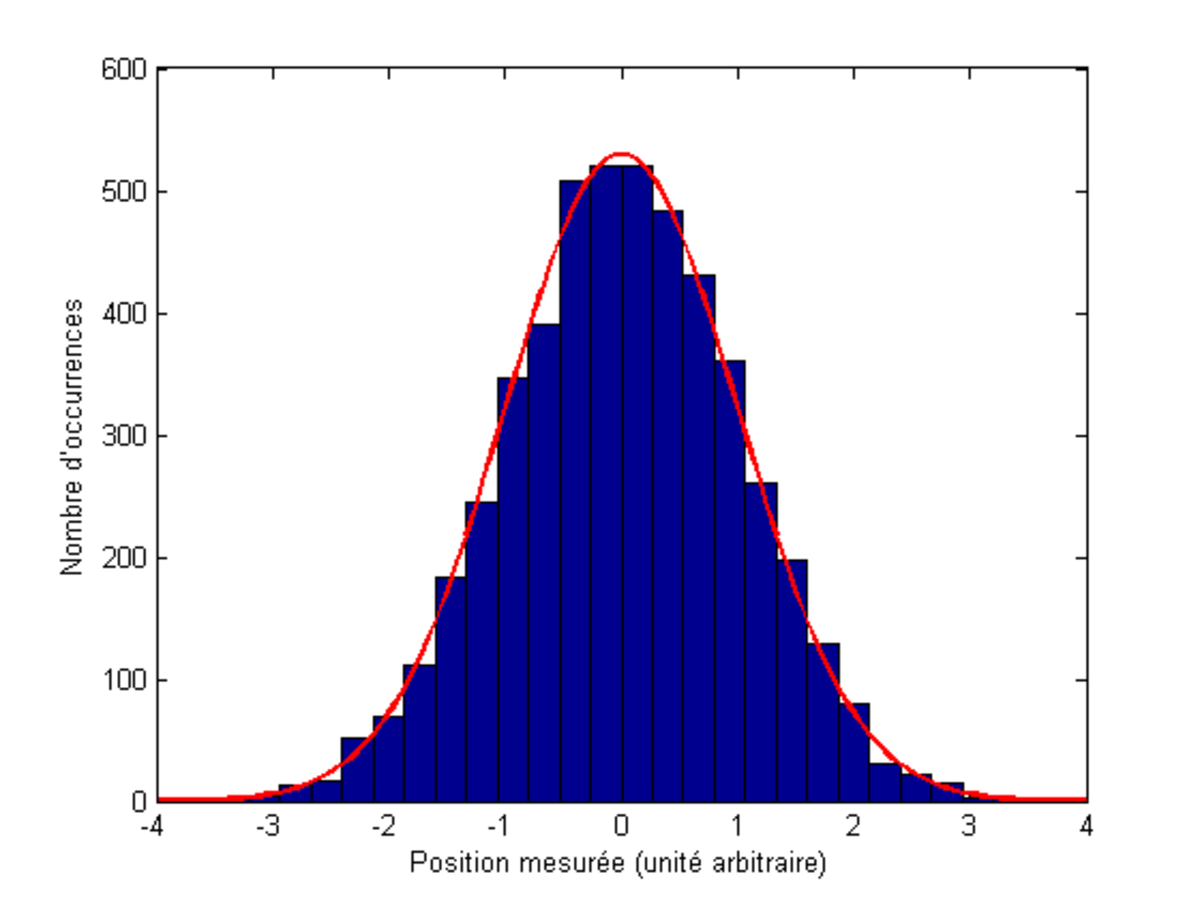
Au cours du temps, les physiciens ont acquis la conviction que ce fait expérimental n'était pas dû à une incertitude expérimentale lors de la mesure, ou encore à une préparation aléatoire d'une fois sur l'autre (dans un état i'i), mais plutôt qu'il n'était pas possible de déterminer l'état par une mesure, aussi complète et précise soit-elle.

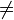
Il n'est cependant pas vain d'espérer gagner de l'information sur l'état i de la particule. On peut y parvenir en effectuant un grand nombre de mesures telles que celle décrite ci-dessus, où la même particule est préparée un grand nombre de fois dans l'état i et sa position est à chaque fois mesurée. En traitant statistiquement les valeurs obtenues, il apparaît que certaines sont obtenues plus fréquemment que d'autres. Ainsi, si la valeur obtenue à l'issue de chaque mesure individuelle n'est pas connue, il est possible de faire des prévisions probabilistes sur les résultats de mesure. Un état détermine donc la distribution de probabilité associée à chacune des observables du système, et réciproquement il est déterminé si l'on sait prédire les distributions de probabilité expérimentales. Il est alors possible de définir des grandeurs statistiques telles que la valeur moyenne de la position ou encore l'écart type de la position (notées " /> et respectivement dans le cas de la position, et < O > et ΔO dans le cas d'une observable O quelconque, ΔO étant également appelée incertitude sur la grandeur O lorsque la particule est dans l'état i).

Mesure de la position d'un ensemble de particules dans une superposition d'états.

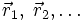
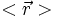
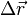
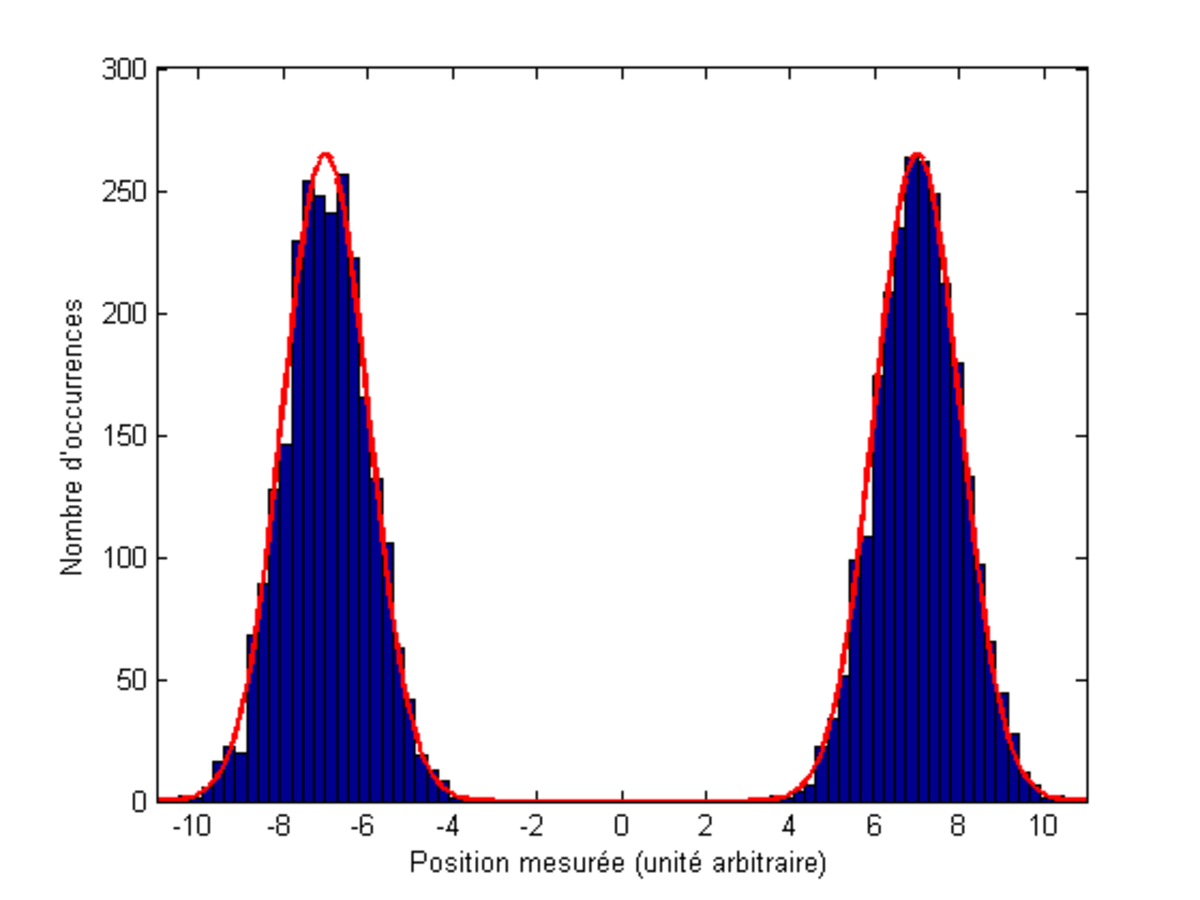
Un cas particulier intéressant correspond à des états pour lesquels l'incertitude ΔO = 0 pour une des observables O. On retrouve alors la prévision de la mécanique classique : dans un de ces états, la mesure de O donnera toujours le même résultat. Pour distinguer ces états là des autres états, ils sont appelés états propres de l'observable O. Les états propres de l'énergie totale présentent l'intérêt de ne pas évoluer au cours du temps : si une particule est dans un état d'énergie donnée, elle restera dans cet état par la suite.

Enfin, un dernier cas particulier permet de préciser ce qui est sous-entendu lorsque l'on dit qu'une particule est dans deux états simultanément. On peut imaginer un état où la distribution de probabilité de la grandeur O est piquée sur deux valeurs. En fait, la particule n'est en réalité que dans un seul état, mais cet état quantique donnera deux résultats possibles lors d'une mesure de O.

Représentation mathématique d'un état

En mécanique quantique, on représente l'état d'un système par un vecteur dans un espace vectoriel hilbertien ; l'espace à considérer dépendant du système étudié. La notation bra-ket permet de représenter les états quantiques de manière concise et simple.

Lorsque l'on associe deux systèmes pour en faire un seul, l'espace des états de ce système composé est le produit tensoriel des espaces des états associés aux deux sous-systèmes.

On retrouve le déterminisme de la mécanique classique dans l'évolution de l'état quantique. C'est-à-dire que l'on peut calculer de manière déterministe comment l'état d'un système va évoluer au cours du temps (grâce à l'équation de Schrödinger), sauf lorsqu'il y a une mesure de l'état de notre système, auquel cas l'évolution n'est plus déterministe, mais probabiliste.

Il s'agit là d'une différence majeure avec la mécanique classique, qui découle du postulat de réduction du paquet d'onde et qui permet de donner une interprétation probabiliste aux états quantiques.

Notons qu'il existe d'autres représentations mathématiques de l'état quantique d'un système, la matrice densité étant une généralisation de la représentation exposée ici.

Interprétation probabiliste des états quantiques

Supposons qu'un système quantique se trouve dans un état et que l'on veuille mesurer une observable du système (énergie, position, spin, ...). Les vecteurs propres de sont notés et les valeurs propres correspondantes α_i, que l'on supposera non dégénérées pour simplifier. Comme le postule le principe de réduction du paquet d'onde, la mesure de A ne peut donner comme résultat que l'un des α_i, et la probabilité d'obtenir le résultat α_i est . Supposons que la mesure donne pour résultat α_p, le système est passé lors de la mesure et de façon instantanée de l'état à l'état .

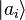
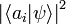
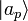
On voit dès lors l'interprétation que l'on peut faire des produits scalaires , où est un état quelconque : en effet, en supposant l'existence d'une observable dont serait un des états propres, on peut dire que la probabilité de trouver le système dans l'état (sous-entendu : si on faisait la mesure) est . Pour cette raison, le produit scalaire est appelé amplitude de probabilité.

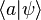
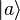
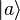
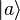
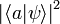
Le fait que la mesure d'une des propriétés du système change l'état de ce système fait que l'on ne peut pas cloner l'état quantique inconnu d'un système. En effet, on pourrait penser qu'en prenant deux systèmes faits des mêmes atomes et en mesurant l'état dans lequel est le système 1, on peut ensuite placer le système 2 dans le même état que le système 1 et ainsi en avoir une copie conforme, mais il faudrait pour cela effectuer plusieurs mesures sur le système 1, dont l'état sera irrémédiablement changé dès la première mesure. Le théorème de non clonage est la base des techniques de cryptographie quantique. La téléportation quantique, quant à elle, cherche à transporter de façon destructive l'état du système 1 sur le système 2.

Superposition d'états, intrication et paradoxe de la mesure

Si |a > et |b > sont deux états possibles du système, i.e. appartiennent à l'espace des états, la définition d'un espace vectoriel fait que toute combinaison linéaire de ces états sera un état possible du système. Pour illustrer l'étrangeté de ces superpositions d'états, Erwin Schrödinger a avancé le paradoxe du chat de Schrödinger : que penser d'un chat que l'on aurait mis dans la superposition d'état

Est-ce le fait qu'il y ait un observateur présent pour tenter de faire une mesure qui réduit le paquet d'onde instantanément à un et un seul des résultats possibles de la mesure ? Quelle est la particularité qui fait qu'un système quantique n'obéisse plus à l'équation déterministe de Schrödinger lors de l'interaction avec un appareil de mesure (ou plus généralement avec un objet macroscopique) ?

Bref, le principe de réduction du paquet d'onde dérange et contribue beaucoup à la réputation de la mécanique quantique d'être contre-intuitive. Après avoir suivi l'école de Copenhague pendant des dizaines d'années, la majorité des physiciens pense aujourd'hui que l'intrication et la décohérence jouent un grand rôle dans l'explication du phénomène de réduction du paquet d'onde. Expérimentalement, il devient possible aujourd'hui de réaliser les expériences de pensée du début du XX^e siècle et des groupes de recherche tentent de réaliser de petits " chats de Schrödinger ", c'est-à-dire des objets mésoscopiques placés dans une superposition d'états pour étudier leur évolution. Pour décrire l'état quantique d'un objet intriqué, l'approche présentée ici à partir de la notation bra-ket n'est pas suffisante, et il convient d'utiliser le formalisme de la matrice densité.