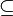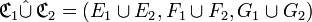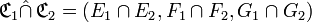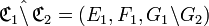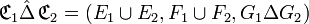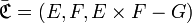Opération sur des correspondances - Définition

Introduction

Une opération sur des correspondances permet de créer de nouvelles correspondances.

Correspondances et opérations ensemblistes

Les opérations purement ensemblistes sur les correspondances n’offrent aucun intérêt. Par exemple, la réunion ensembliste de deux correspondances n’est pas en général une correspondance.

En revanche, il est possible de définir des correspondances dont le graphe est le résultat d’opérations ensemblistes sur d’autres graphes :

Réunion

La réunion relationnelle de deux correspondances et , notée :

«  »   ( lire « C1 union C2 » )

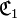
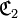
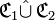
est la correspondance dont :

- l’ensemble de départ est la réunion des ensembles de départ des deux correspondances,

- l’ensemble d’arrivée est la réunion de leurs ensembles d’arrivée,

- et le graphe est la réunion de leurs graphes.

En d’autres termes, si et si , alors :

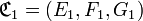
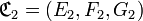
Intersection

L’intersection relationnelle de deux correspondances et , notée :

«  »   ( lire « C1 inter C2 » )

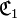
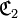
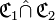
est la correspondance dont :

- l’ensemble de départ est l’intersection des ensembles de départ des deux correspondances,

- l’ensemble d’arrivée est l’intersection de leurs ensembles d’arrivée,

- et le graphe est l’intersection de leurs graphes.

En d’autres termes, si et si , alors :

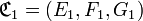
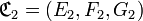
Différence

La différence relationnelle de deux correspondances et , notée :

«  »   ( lire « C1 moins C2 » )

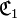
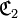
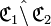
est la correspondance dont :

- l’ensemble de départ est l’ensemble de départ de la première correspondance,

- l’ensemble d’arrivée est l’ensemble d’arrivée de cette correspondance,

- et le graphe est la différence des graphes des deux correspondances.

En d’autres termes, si et si , alors :

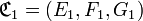
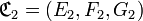
Différence symétrique

La différence symétrique relationnelle de deux correspondances et , notée :

«  »   ( lire « C1 delta C2 » )

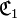
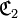
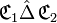
est la correspondance dont :

- l’ensemble de départ est la réunion des ensembles de départ des deux correspondances,

- l’ensemble d’arrivée est la réunion de leurs ensembles d’arrivée,

- et le graphe est la différence symétrique de leurs graphes.

En d’autres termes, si et si , alors :

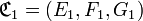
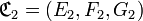
Complémentaire

La correspondance complémentaire relationnelle d’une correspondance , notée :

«   »   ( lire « C barre » )

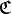
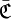
est la correspondance dont :

- l’ensemble de départ est celui de ,

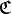
- l’ensemble d’arrivée est celui de ,

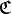
- et le graphe est le complémentaire de celui de dans le produit cartésien des ensembles de départ et d’arrivée.

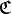
En d’autres termes, si , alors :

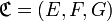
Par exemple, la correspondance complémentaire d’une correspondance vide est une correspondance pleine, et vice versa car : .

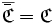
Il ne faut pas confondre les correspondances complémentaires et réciproques. Ainsi, la réciproque d’une correspondance vide est elle-même vide, alors que sa complémentaire est une correspondance pleine.

Remarque importante

En pratique, quand nous rencontrerons une opération ensembliste sur des correspondances, il s’agira en fait d’un abus de langage : par exemple, l’intersection «   » désignera en fait l’intersection relationnelle «   » . Cet abus de langage est sans conséquence puisque les véritables opérations ensemblistes sur les correspondances n’offrent pas d’intérêt. De plus, il rejoint et renforce celui consistant à confondre les correspondances avec leur graphe.

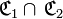
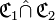
Comparaison de correspondances

L’abus de langage précédent s’étend à l'inclusion des correspondances : nous définissons l'inclusion relationnelle de deux correspondances par l’inclusion de leurs ensembles de départ, d’arrivée et graphes respectifs.

En d’autres termes, si et si , alors :

.

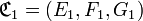
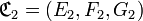
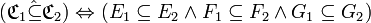
Là encore, en pratique, nous parlons d'« inclusion » au lieu d'« inclusion relationnelle » et nous notons «   » au lieu de «   ».