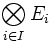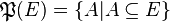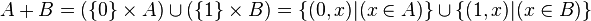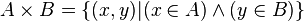Opération ensembliste - Définition

Introduction

Les opérations ensemblistes sont les opérations mathématiques faites sur les ensembles, sans s’occuper de la nature des éléments qui composent ces ensembles. Les opérations booléennes (réunion, intersection, complémentaire ...) sont traitées dans l'article algèbre des parties d'un ensemble.

Ensemble des parties

L’ensemble des parties d'un ensemble E, noté habituellement (E) ou (E), est, comme son nom l’indique, l’ensemble formé par tous les sous-ensembles de l’ensemble E:

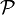
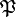
Par exemple si A = {a,b}, (A)={Ø,{a},{b},A}

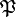
L’existence de l’ensemble des parties est assurée par un axiome, l’axiome de l'ensemble des parties. Cet axiome exprime en substance que pour tout ensemble E, il existe un ensemble F contenant tous les sous-ensembles de E.

L’unicité de l’ensemble des parties est assurée par un autre axiome, l’axiome d'extensionnalité.

L’ensemble des parties d’un ensemble, muni de la réunion, de l’intersection et de l’inclusion forme une algèbre de Boole.

L’ensemble des parties d’un ensemble, muni de la différence symétrique et de l’intersection forme un corps commutatif. Si l'ensemble de départ est fini, avec n éléments, alors ce corps est isomorphe à   , corps fini à 2ⁿ éléments.

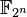
Somme disjointe

La différence symétrique de deux ensembles A et B ne doit pas être confondue avec leur somme disjointe, notée , ou encore  :

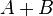
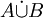
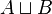
Les symboles et dans la définition précédente peuvent être remplacés par d’autres, par exemple et . La seule exigence est que les deux symboles utilisés diffèrent l’un de l’autre.

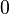
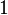
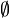
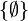
La somme disjointe permet de définir la somme de cardinaux  :

card(A) + card(B) = card(A + B)

Produit cartésien

Le produit cartésien, noté (lire « A croix B »), de deux ensembles A et B est l’ensemble des couples dont la première composante vient de A et la seconde de B :

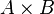
On a pour A et B finis:

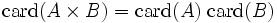
Exponentiation

On définit comme l’ensemble des applications de E dans F.

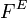
On peut alors identifier l’ensemble des parties d’un ensemble E, , à  ; cela revient en effet à identifier chaque partie de E à son indicatrice.

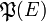
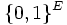
On peut aussi considérer le produit cartésien comme étant l’ensemble E^I.