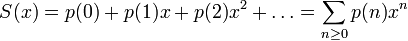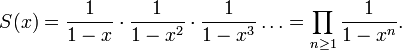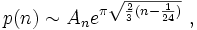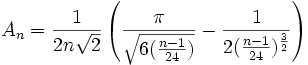Partition d'un entier - Définition

Relations

Relation d'ordre

L'ensemble des partitions de n est muni d'un ordre lexicographique, c'est-à-dire que si deux partitions sont représentées par des suites décroissantes qui coïncident jusqu'au rang k exclu, alors celle qui a un plus grand terme au rang k est supérieure à l'autre, quels que soient leur nombre de termes et leurs valeurs ensuite.

La partition composée du seul terme n est donc supérieure à toutes les autres partitions de n, tandis que la plus petite est celle qui est composée de n termes qui valent tous 1.

Cet ordre est total, c'est-à-dire que toutes les partitions d'un même entier peuvent être comparées entre elles.

Dualité

Le fait de lire en lignes un diagramme de Ferrers tracé en colonnes, ou réciproquement, permet de définir la partition duale (ou conjuguée). Géométriquement, ce la revient à effectuer une symétrie par rapport à la diagonale. En particulier, cela implique que cette dualité est involutive : toute partition est duale de sa partition duale.

Formellement, si une partition est représentée par une suite finie λ = (λ_i), la partition duale est définie par la suite λ ^* où λ ^* _k est le nombre de termes de λ supérieurs ou égaux à k.

La dualité permet de montrer de mettre en évidence une bijection entre l'ensemble des partitions en exactement k parties et l'ensemble des partitions dont la première partie (la plus grande) est k. Cette propriété est à la base d'une formule récursive permettant de dénombrer les partitions d'un entier (voir ).

Partition autoduale

Une partition qui est égale à sa partition duale est dite autoduale ou autoconjuguée. Un exemple simple de partition autoduale est donné par un diagramme en 'L', définis pour tout entier impair de la forme 2k + 1, avec une première partie valant k et toutes les autres valant 1. D'autres exemples sont donnés pour les carrés et les nombres triangulaires.

La représentation par les diagramme de Ferrers permet de prouver que l'ensemble des partitions autoduales est en bijection avec l'ensemble des partitions à parties impaires distinctes. En effet, le diagramme de chaque partition autoduale peut être décomposé en une suite de diagrammes en 'L' de taille strictement décroissante mais toujours impaire. Réciproquement, les parties impaires d'une partition (à parties distinctes) peuvent être associées à des diagrammes en 'L', dont la juxtaposition dans l'ordre décroissant forme le diagramme de Ferrers d'une partition autoduale.

Injections

Les diagrammes de Ferrers permettent de visualiser certaines relations entre les ensembles de partitions d'entiers. Notamment, l'adjonction d'une partie valant 1 induit une injection de l'ensemble des partitions d'un entier dans l'ensemble des partitions de l'entier suivant. Un autre exemple est donné par l'incrémentation de toutes les parties, qui induit une injection de l'ensemble des partitions d'un entier n en k parties, dans l'ensemble des partitions de (n + k) en k parties.

Suite des nombres de partitions

Propriétés

Les techniques des diagrammes de Ferrers permettent aussi de prouver des résultats comme le suivant :

• Il y a p(n) - p(n-1) partages de n dans lesquels chaque partie est supérieure à 2.
• p(1) + p(2) + ... + p(n) < p(2n)

Il a été démontré que si n se termine par 4 ou 9, alors p(n) est divisible par 5.

• p(1) = 1
• p(2) = 2
• p(3) = 3
• p(4) = 5
• p(5) = 7
• p(6) = 11
• p(7) = 15
• p(8) = 22
• p(9) = 30
• p(10) = 42
• p(50) = 204226
• p(100) = 190 569 292
• p(200) = 3972999029388
• p(1 000) = 24061467864032622473692149727991
• p(10 000) = 36167251325636293988820471890953695495016030339315650422081868605887952568754066420592310556052906916435144

Fonction génératrice associée

Euler a remarqué (sans trop se soucier de considérations de convergence) que la série génératrice de p,

est égale au produit infini suivant :

En effet, en développant chaque facteur comme une série géométrique, le produit infini se réécrit :

(1 + x + x² + x³ + ...)(1 + x² + x⁴ + x⁶ + ...)(1 + x³ + x⁶ + x⁹ + ...)...

et le coefficient du terme de degré n est le nombre de suites d'exposants dont la somme vaut n, chaque exposant étant un multiple de son rang. Ces suites correspondent à la définition des partitions d'un entier sous forme d'une mesure (voir ).

La formulation de la fonction génératrice est similaire à la formulation du produit de plusieurs formes modulaires, en donnant une certaine idée de la connexion entre les deux.

Estimation asymptotique

Hardy et Ramanujan ont présenté en 1918 une fonction approximative de p(n) ; à savoir :

quand

La correction très énigmatique , inventée par Ramanujan, fait que p(200) est exact !

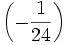
Plus tard, ils obtinrent une égalité stricte pour calculer p(n).

Série de Rademacher

En affinant la méthode employée par Hardy et Ramanujan, Rademacher démontra en 1937 la formule suivante:

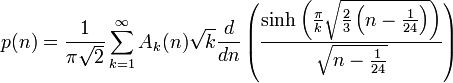
avec et s(h,k) la somme de Dedekind. Le démonstration de cette formule fait intervenir les suites de Farey, les cercles de Ford, et l'analyse complexe.