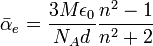Polarisabilité - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En électromagnétisme et en chimie, la polarisabilité désigne un phénomène causé par le moment des charges électriques de l'atome.
Une molécule placée dans un champ électrique
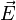
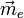
Dans les molécules di ou polyatomiques, les atomes se déplacent également les uns par rapport aux autres d'où une contribution supplémentaire dite atomique. Pour les champs faibles, le moment induit est proportionnel au champ, d'où la relation
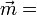

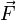

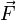
La polarisabilité est donc la somme de deux contributions. La première, de loin la plus importante, est la polarisabilité électronique. La polarisabilité atomique joue un rôle mineur, quoique non négligeable.
Généralités
- Dans le référentiel principal de la molécule, le tenseur des polarisabilités est diagonal.
- La polarisabilité électronique mesurée (via des mesures d'indice de réfraction et de densité) est la moyenne de ces éléments diagonaux.
- Dans le Système international, les polarisabilités sont exprimées en C2m2J − 1
- Dans le système UES et CGS, les polarisabilités sont exprimées en A3. Elles ont la dimension d'un volume.
- La polarisabilité atomique augmente avec la taille des atomes (par extension, les anions seront donc plus polarisables que les atomes neutres correspondant).
Polarisabilté atomique
Dans une molécule quelconque il existe une seconde contribution
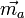
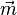
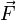
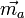
La relation tensorielle entre
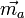
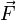
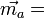
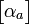
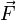
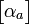
La contribution atomique est relativement faible devant la polarisabilité électronique. Pour les molécules courantes on estime que le rapport
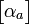
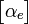
Polarisabilté électronique
Notion tensorielle de la polarisabilité
Dans le cas d'un atome le moment induit
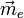
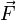
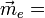
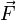
Dans le cas d'une molécule, le moment induit
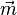
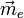
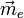
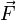
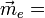
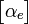
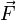
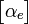
Comme c'est un tenseur symétrique il est déterminé par la donnée de 6 éléments. Dans le repère principal de la molécule ce tableau devient diagonal et les termes diagonaux sont les polarisabilités principales de la molécule
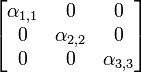
La relation qui relie le moment induit et le champ local
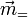

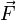
| mi = | ∑ | αi,jFj |
| j |
où mi est la composante de
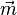
Dans un repère quelconque le tenseur
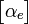
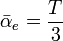
Le second invariant est l'anisotropie de polarisabilité notée γ2. Cette grandeur mesure la différence entre les différentes composantes du tenseur des polarisabilités. Dans le référentiel principal, on écrit :
Mesure de la polarisabilité électronique
On déduit
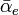
avec NA le nombre d'Avogadro, ε0 la permittivité du vide, M la masse molaire de la molécule étudiée, n et d les indice de réfraction et la densité du liquide correspondant.
Dans le Système international, les polarisabilités sont exprimées en C2m2J − 1. Dans le système d'unité UES CGS, elles sont exprimées comme un volume en 1A3 avec 1A3 = 1,112761.10 − 41C2m2J − 1
Mesure de l'anisotropie des polarisabilités électroniques
On déduit γ2 des mesures de diffusion de la lumière (ou diffusion Rayleigh) ou d'effet Kerr. Cette grandeur s'exprime en A6 dans le système ues cgs.

![\gamma^2 = \frac 12[(\alpha_{1,1} - \alpha_{2,2})^2 + (\alpha_{1,1} - \alpha_{3,3})^2 + (\alpha_{2,2} - \alpha_{3,3})^2 ]](https://static.techno-science.net/illustration/Definitions/autres/c/ccd1cef62405d1bcf358b8044cc63a55_b5d5e685a06a5a216d9d3d5b9178520e.png)