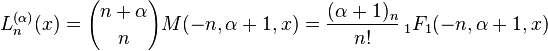Polynôme de Laguerre - Définition
Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
La liste des auteurs de cet article est disponible ici.
Relation aux fonctions hypergéométriques
Les polynômes de Laguerre peuvent être reliés aux fonctions hypergéométriques, plus précisément aux fonctions hypergéométriques confluentes, par
où (a)n est le symbole de Pochhammer (qui, dans ce cas particulier, est utilisé pour représenter la factorielle croissante a(a + 1)(a + 2)...(a + n − 1)).