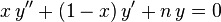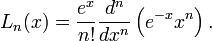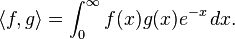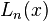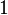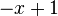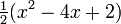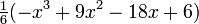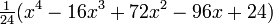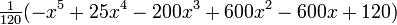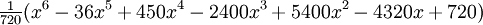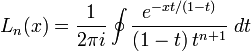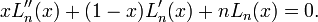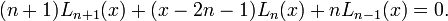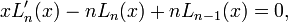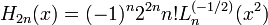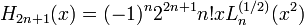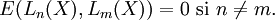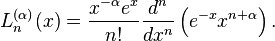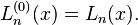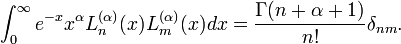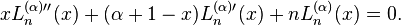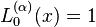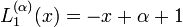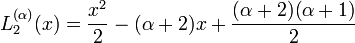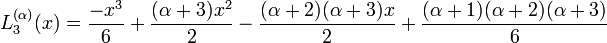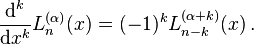Mercredi 11 Décembre 2024
Rechercher 🔍

Polynôme de Laguerre - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.
- Introduction - Les quelques premiers polynômes - Expression par une intégrale de contour - Propriétés - Relation aux polynômes d'Hermite - Polynômes de Laguerre généralisés - Relation aux fonctions hypergéométriques

Introduction

En mathématiques, les polynômes de Laguerre, nommés d'après Edmond Laguerre (1834 - 1886), sont les solutions de l'équation de Laguerre :

x\,y'' + (1 - x)\,y' + n\,y = 0\,

qui est une équation différentielle linéaire du second ordre. Cette équation a des solutions non singulières seulement si n est un entier positif.

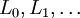
Ces polynômes, traditionnellement notés L_0, L_1, \dots , forment une suite de polynômes qui peut être définie par la formule de Rodrigues

L_n(x)=\frac{e^x}{n!}\frac{d^n}{dx^n}\left(e^{-x} x^n\right).

Ils sont orthogonaux les uns par rapport aux autres pour le produit scalaire défini par

\langle f,g \rangle = \int_0^\infty f(x) g(x) e^{-x}\,dx.

La séquence des polynômes de Laguerre est une suite de Sheffer.

Les polynômes de Laguerre apparaissent en mécanique quantique dans la partie radiale de la solution de l'équation de Schrödinger pour un atome à un électron.

Les physiciens utilisent souvent une définition des polynômes de Laguerre où les polynômes sont multipliés par un facteur (n!) par rapport à la définition donnée ici.

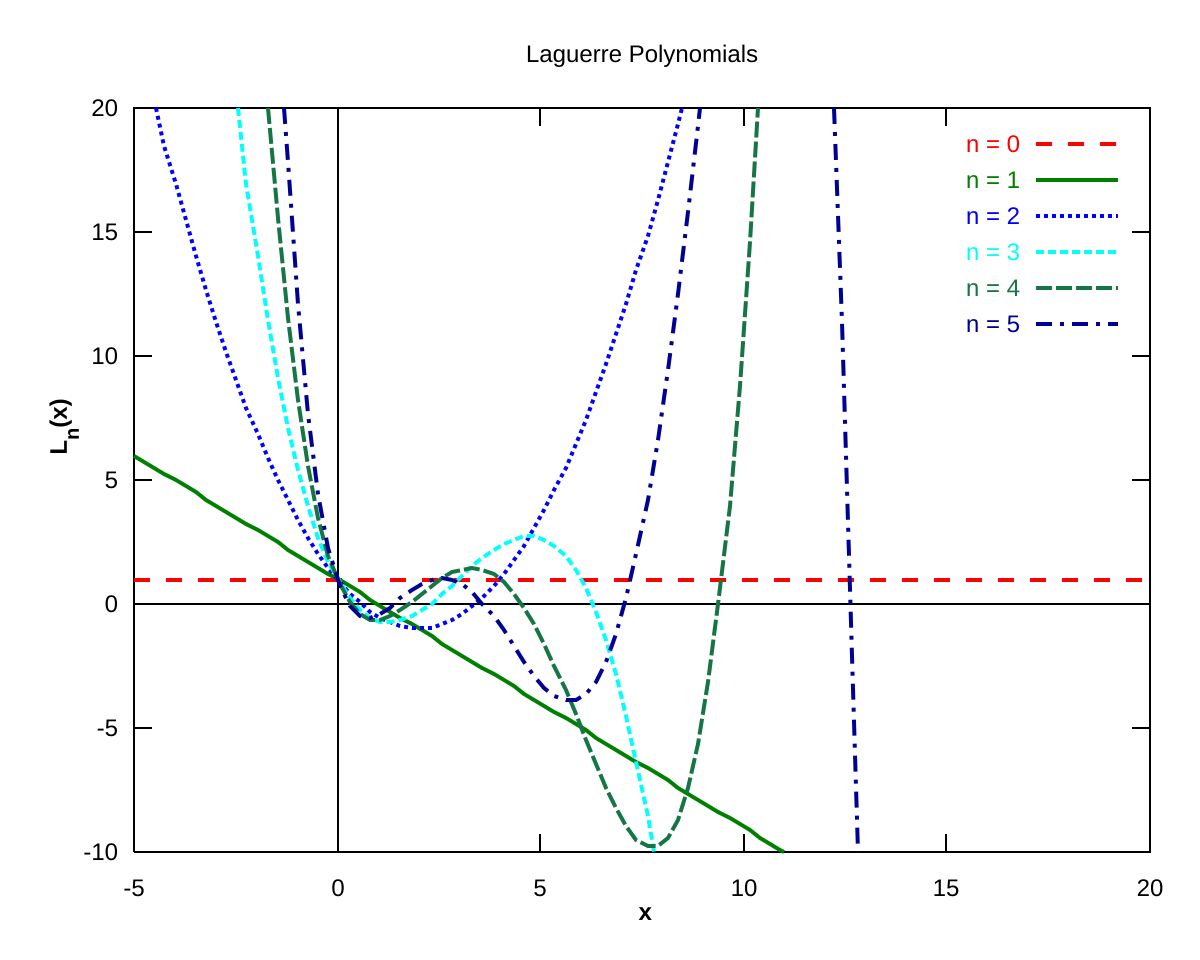
Les quelques premiers polynômes

Voici les premiers polynômes de Laguerre:

n L_n(x)\,
0 1\,
1 -x+1\,
2 \begin{matrix}\frac12\end{matrix} (x^2-4x+2) \,
3 \begin{matrix}\frac16\end{matrix} (-x^3+9x^2-18x+6) \,
4 \begin{matrix}\frac1{24}\end{matrix} (x^4-16x^3+72x^2-96x+24) \,
5 \begin{matrix}\frac1{120}\end{matrix} (-x^5+25x^4-200x^3+600x^2-600x+120) \,
6 \begin{matrix}\frac1{720}\end{matrix} (x^6-36x^5+450x^4-2400x^3+5400x^2-4320x+720) \,
Les 6 premiers polynômes de Laguerre.

Expression par une intégrale de contour

Les polynômes peuvent être exprimés en termes d'une intégrale de contour

L_n(x)=\frac{1}{2\pi i}\oint\frac{e^{-xt/(1-t)}}{(1-t)\,t^{n+1}} \; dt

où le contour entoure l'origine une fois dans le sens trigonométrique.

Propriétés

La fonction génératrice pour les polynômes de Laguerre est

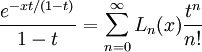
\frac{e^{-xt/(1-t)}}{1-t} = \sum_{n=0}^\infty L_n(x) \frac{t^n}{n!}\, .

Le n-ième polynôme de Laguerre satisfait l'équation différentielle suivante :

x L_n''(x)+ (1-x)L_n'(x)+ n L_n(x)=0.\,

On a aussi la suite récurrente suivante :

(n+1)L_{n+1}(x)+ (x-2n-1) L_{n}(x)+nL_{n-1}(x)=0.\,

Les polynômes satisfont la propriété

x L_n'(x)-nL_{n}(x)+nL_{n-1}(x)=0,\,

Relation aux polynômes d'Hermite

Les polynômes de Laguerre généralisés apparaissent dans le traitement de l'oscillateur harmonique quantique, à cause de leur relation aux polynômes d'Hermite, qui peuvent être exprimés par

H_{2n}(x) = (-1)^n 2^{2n} n! L_n^{(-1/2)} (x^2)

et

H_{2n+1}(x) = (-1)^n 2^{2n+1} n! x L_n^{(1/2)} (x^2)

où les Hn(x) sont les polynômes d'Hermite.

Polynômes de Laguerre généralisés

La propriété d'orthogonalité évoquée plus haut revient à dire que si X est une variable aléatoire distribuée exponentiellement avec la fonction densité de probabilité

f(x)=\left\{\begin{matrix} e^{-x} & \mbox{si}\ x>0, \\ 0 & \mbox{si}\ x<0, \end{matrix}\right.

alors

E(L_n(X),L_m(X))=0\ \mbox{si}\ n\neq m.

La distribution exponentielle n'est pas la seule distribution Gamma. Une séquence polynomiale orthogonale par rapport à la distributoin gamma dont la fonction densité de probabilité est, pour α > − 1,

f(x)=\left\{\begin{matrix} x^\alpha e^{-x}/\Gamma(1+\alpha) & \mbox{si}\ x>0, \\ 0 & \mbox{si}\ x<0, \end{matrix}\right.

(cf.fonction gamma) est donnée par l'équation de Rodrigues pour les polynômes de Laguerre généralisés:

L_n^{(\alpha)}(x)= {x^{-\alpha} e^x \over n!}{d^n \over dx^n} \left(e^{-x} x^{n+\alpha}\right) .

Ils sont parfois appelés les polynômes de Laguerre associés. On retrouve les polynômes de Laguerre simples en prenant α = 0:

L^{(0)}_n(x)=L_n(x).

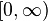
Les polynômes de Laguerre généralisés sont orthogonaux sur [0,\infty) par rapport à la fonction de poids xαe − x:

\int_0^{\infty}e^{-x}x^\alpha L_n^{(\alpha)}(x)L_m^{(\alpha)}(x)dx=\frac{\Gamma(n+\alpha+1)}{n!}\delta_{nm}.

Les polynômes de Laguerre généralisés obéissent à l'équation différentielle

x L_n^{(\alpha) \prime\prime}(x) + (\alpha+1-x)L_n^{(\alpha)\prime}(x) + n L_n^{(\alpha)}(x)=0.\,

Exemples de polynômes de Laguerre généralisés

Les premiers polynômes de Laguerre généralisés sont

L_0^{(\alpha)} (x) = 1
L_1^{(\alpha)}(x) = -x + \alpha +1
L_2^{(\alpha)}(x) = \frac{x^2}{2} - (\alpha + 2)x + \frac{(\alpha+2)(\alpha+1)}{2}
L_3^{(\alpha)}(x) = \frac{-x^3}{6} + \frac{(\alpha+3)x^2}{2} - \frac{(\alpha+2)(\alpha+3)x}{2} + \frac{(\alpha+1)(\alpha+2)(\alpha+3)}{6}

Dérivées des polynômes de Laguerre généralisés

En différentiant la représentation en série d'un polynôme de Laguerre généralisé k fois conduit à

\frac{\mathrm d^k}{\mathrm d x^k} L_n^{(\alpha)} (x) = (-1)^k L_{n-k}^{(\alpha+k)} (x)\,.
Relation aux fonctions hypergéométriques
- Introduction - Les quelques premiers polynômes - Expression par une intégrale de contour - Propriétés - Relation aux polynômes d'Hermite - Polynômes de Laguerre généralisés - Relation aux fonctions hypergéométriques
miniature
Le télescope James Webb, poussé à ses limites, découvre ces structures incroyablement anciennes 🔭
miniature
Le rôle surprenant de la grossesse contre la grippe A 🦠
miniature
Découverte d'une nouvelle espèce éteinte grâce à... un accélérateur de particules ⚛️
miniature
Une avancée prometteuse pour le déploiement des batteries sodium-ion 🔋
miniature
Voici comment et pourquoi le risque de cancer augmente... puis diminue avec l'âge 🧬
miniature
Le Soleil bientôt en "zone de combat": une période de turbulences extrêmes ☀️
miniature
Les rhumatismes plus douloureux par temps humide: vrai ou faux ? 🌧️
miniature
Ce nouveau type de moteur repousse les limites du vol supersonique ✈️
miniature
Poster sur les réseaux sociaux peut nuire à votre santé mentale 🧠
miniature
Une super-Terre entre Mars et Jupiter ? 🌎
miniature
Découverte impressionnante d'un fossile de crocodile géant 🐊
miniature
1
Cet accident en laboratoire pourrait transformer drastiquement la mémoire numérique ⚡
miniature
Un virage technologique révèle l'impact du diabète gestationnel 🩺
miniature
Insolite: ces loups butinent des fleurs ! Des grands carnivores pollinisateurs ? 🌼
miniature
1
Ce fin gilet robotisé soulage les tâches répétitives 🦾
miniature
Les équations d'Einstein invalidées ? 👀
miniature
Ce tatouage électronique se connecte à votre cerveau 🧠
miniature
Cette IA de Google prédit la météo mieux que jamais, et sur 15 jours ! 🌦️
miniature
Des plats au bœuf... sans bœuf ? 🥩
miniature
2
Ce moteur de recherche d'un nouveau genre bouscule nos habitudes 🔍
miniature
Pourquoi les cheveux bouclent-ils en fonction de la météo ? 🌦️
miniature
Découverte: d'autres univers plus propices à la vie que le notre 👽
miniature
Ces sons urbains qui minent notre santé mentale 🚗
miniature
La testostérone impacte-t-elle vraiment le désir sexuel des hommes ? 🔥
miniature
Des microalgues éliminent les métaux lourds: voici comment 🧪
miniature
1
Et voici un qubit mécanique ! 🖥️
miniature
Les lentilles de contact sont-elles vraiment sans danger ? 👁️
miniature
Dans la course à l'IA générative, Google lance son générateur de vidéos 🎥
miniature
4
Une zone oubliée du cerveau permet aux paralysés de marcher à nouveau 🧠
miniature
Cette astuce quotidienne ajoute 11 ans à votre vie 🕒
miniature
Révolutions, migrations des européens... les éruptions volcaniques ont influencé l'histoire 🌋
miniature
Soit l'énergie noire n'est pas constante, soit une seconde force inconnue est à l'œuvre... 🌀
miniature
Voici pourquoi l'alcool peut rendre agressif 🥂
miniature
Expérience inédite: ce laser projette une ombre visible 💥
miniature
Ce plat millénaire réduit significativement la graisse corporelle 🍽️
miniature
Les scientifiques trompés ? La Voie Lactée n'est PAS comme les autres galaxies 🔭
miniature
Pourquoi ce que pensent les autres de nous nous fait tant ruminer ? 🧠
miniature
De la vie découverte sur un échantillon de l'astéroïde Ryugu (oups) 👽
miniature
2
Des anomalies incompréhensibles de températures détectées simultanément presque partout sur Terre 🌡️
miniature
Cette planète, trop jeune pour exister, bouscule les lois de l'astronomie 🪐
miniature
Une montagne d'or découverte en Chine ⛏️
miniature
Cette simulation de l'Univers est totalement vertigineuse 🌀
miniature
1
Une pilule pourrait-elle imiter les bienfaits du yoga ? 🧘
miniature
Nous serions-nous trompés sur l'origine de l'écriture alphabétique ? ✍️
miniature
Voici pourquoi votre enfant triche et ce que cela révèle 🧠
miniature
Le Sahara verdit, et cela pourrait bien (re)changer notre climat 🌱
miniature
1
Neuralink: un bras robotique contrôlé par la pensée 🦾
miniature
Ces fossiles humains à grands crânes seraient-ils une espèce jusqu'alors inconnue ? 💀
miniature
1
L'étonnant impact du froid sur notre sommeil ❄️
miniature
Une base cachée de missiles nucléaires repérée par erreur sous la calotte glacière ☢️
Page générée en 0.155 seconde(s) - site hébergé chez Contabo
Ce site fait l'objet d'une déclaration à la CNIL sous le numéro de dossier 1037632
A propos - Informations légales | Partenaire: HD-Numérique
Version anglaise | Version allemande | Version espagnole | Version portugaise