Prisme (optique) - Définition

Introduction

Un prisme est un élément optique utilisé pour réfracter la lumière, la réfléchir ou la disperser en ses constituants (les différents rayonnements de l'arc-en-ciel pour la lumière blanche). C'est traditionnellement un prisme (solide) droit à base triangulaire, constitué d'un matériau transparent : verre, plexiglas, notamment.

Du point de vue de l'optique géométrique, un prisme est l'association de deux dioptres plans non parallèles.

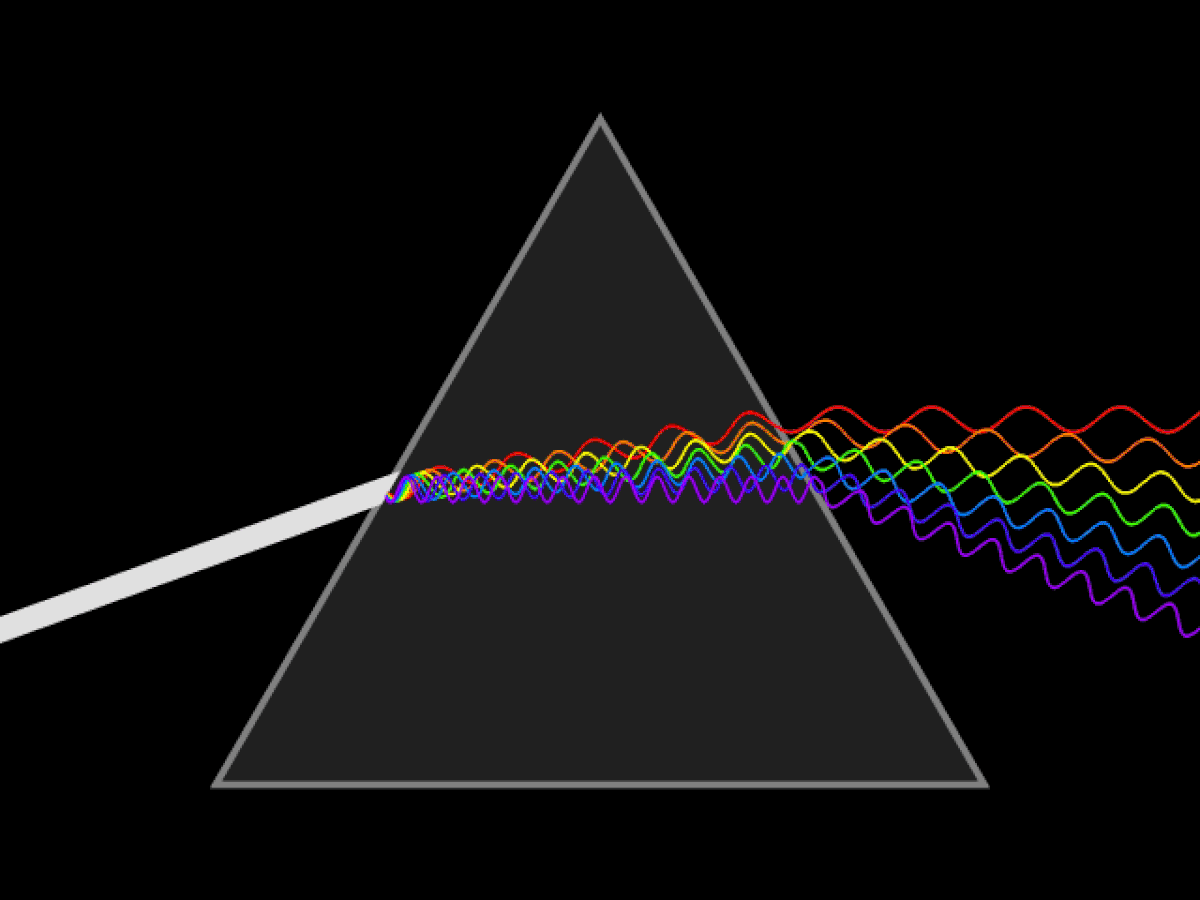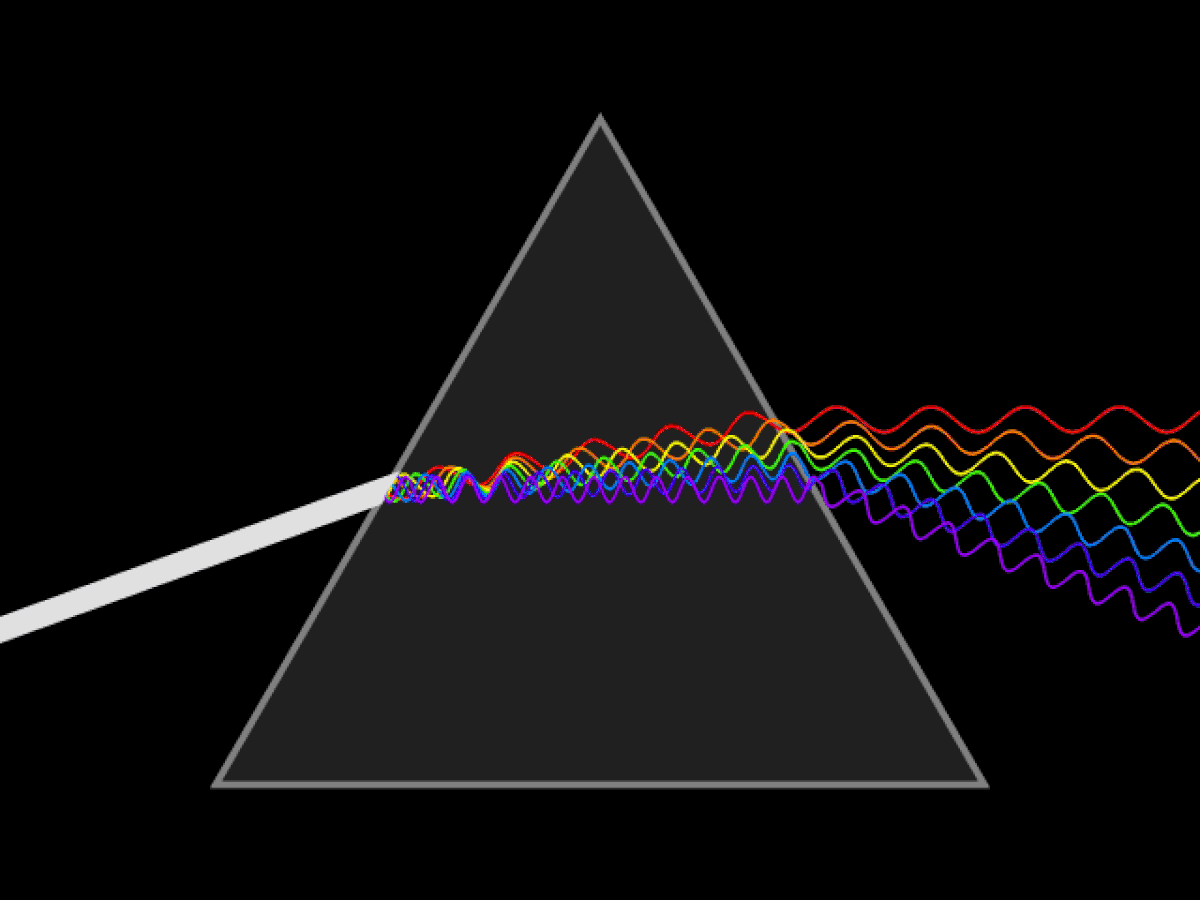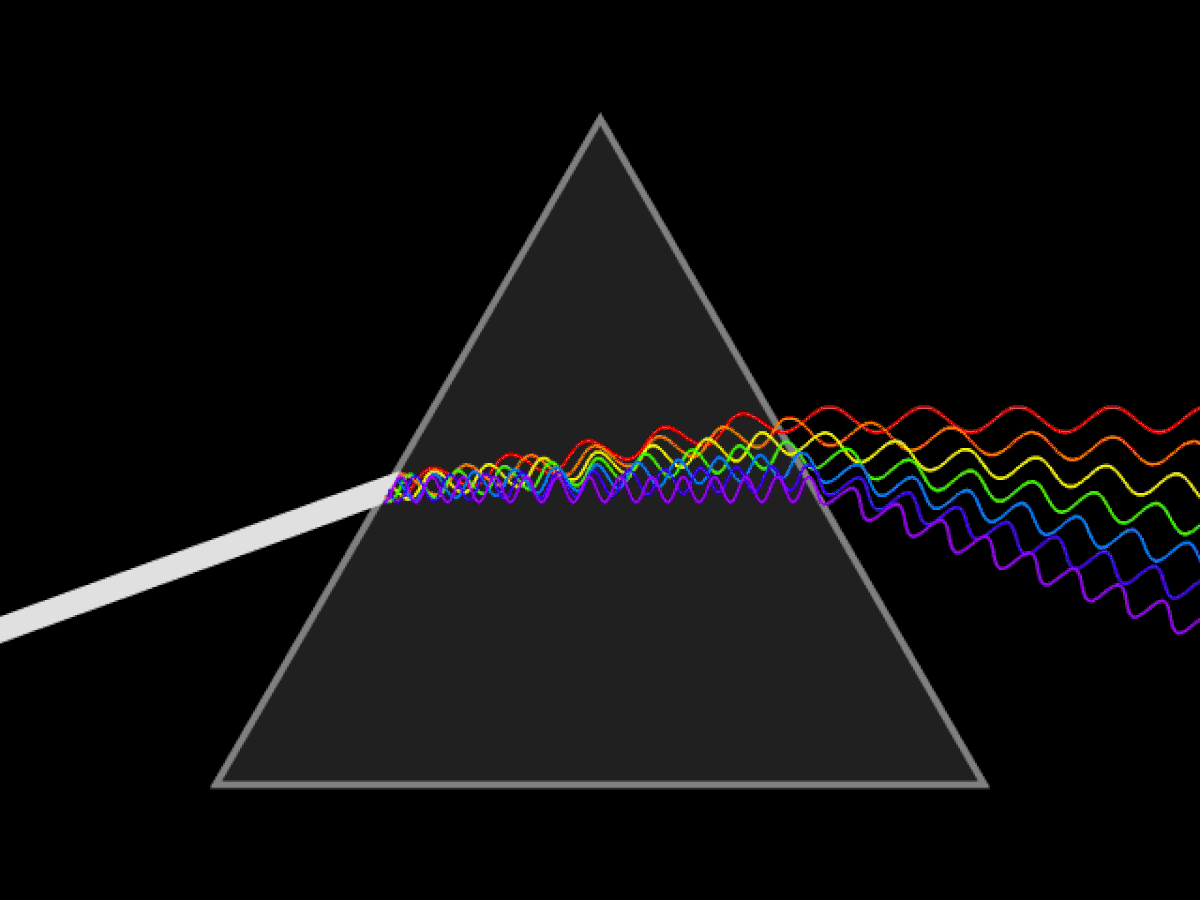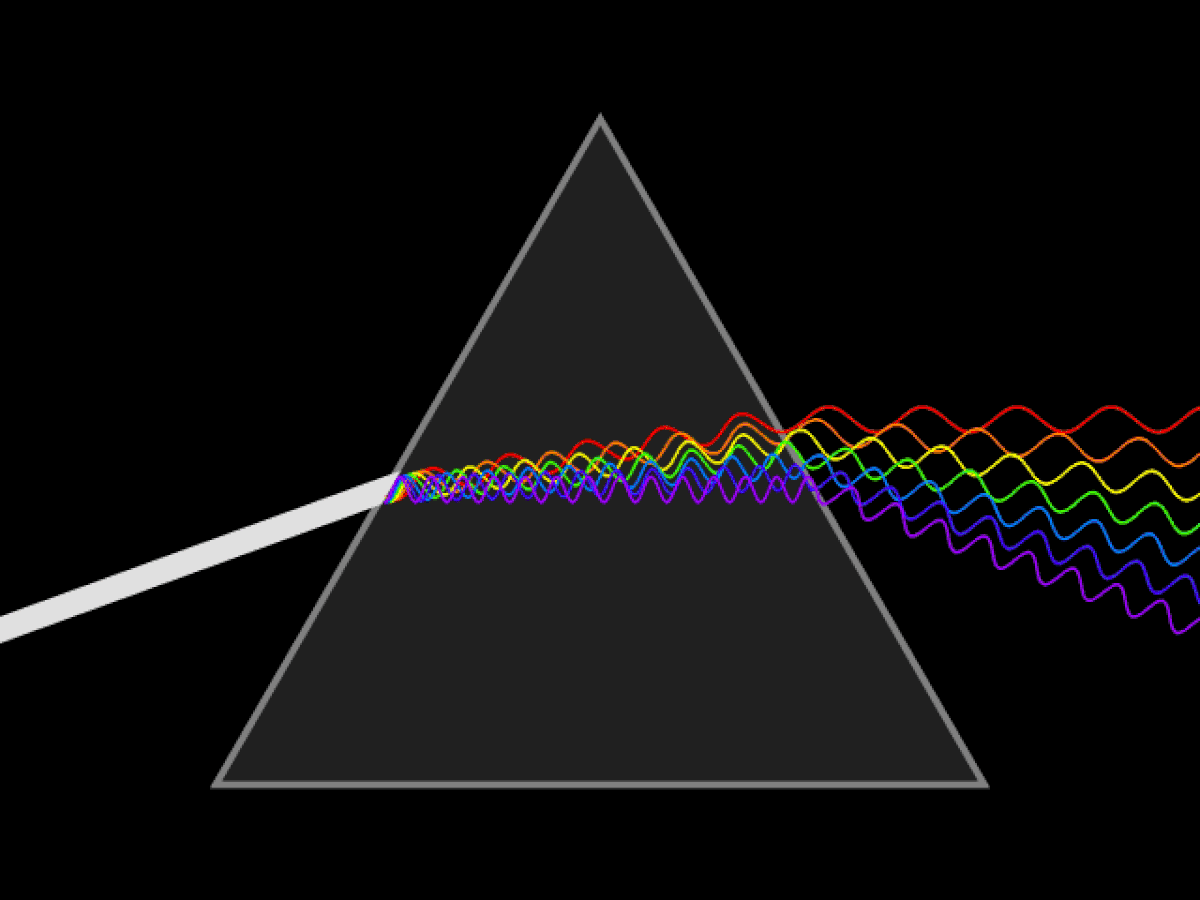
Lorsque la lumière passe de l'air au verre, par exemple, elle est réfractée. Lorsqu'elle ressort par l'autre face, elle est de nouveau réfractée. Le rayon ou faisceau incident est donc dévié. Mais l'indice de réfraction n'est pas le même pour les différentes longueurs d'onde. De sorte que, un faisceau de lumière blanche est séparé en ses composantes : le bleu est plus dévié que le jaune, lui-même plus dévié que le rouge (cf figure 1). Dans ces conditions, le prisme peut être utilisé pour analyser un rayonnement visible polychrome (spectroscopie).

Un peu d'histoire

Avant Isaac Newton, on pensait que le prisme ajoutait des couleurs au faisceau de lumière blanche. Newton place alors un deuxième prisme de telle manière qu'il ne soit atteint que par une seule couleur et découvre que la couleur reste inchangée. Il en conclut que les prismes permettent de disperser les couleurs. Il utilise ensuite un deuxième prisme et réussit à recomposer un faisceau blanc à partir de l'arc-en-ciel généré par le premier prisme : la démonstration était faite que les couleurs ne sont pas le résultat d'une action du prisme sur la lumière blanche, mais bien que c'est la lumière blanche qui est composée de plusieurs couleurs.

Aujourd'hui, on parle de composantes monochromatiques et de spectres lumineux. Le spectre de la lumière solaire est un spectre continu, tandis que le spectre des émissions atomiques (lampe au mercure, au sodium, par exemple) est constitué de raies correspondant à des longueurs d'ondes précises. C'est ce phénomène qui a amené Niels Bohr à imaginer la quantification de l'énergie des atomes, nouvelle physique connue désormais sous le terme de physique quantique.

Dispersion chromatique

L'indice de réfraction d'un verre varie en fonction de la longueur d'onde, ce qui provoque une dispersion chromatique.

D'après la loi de Cauchy, on a :

n(λ) = a + b/λ²

où a et b sont des constantes dépendant du verre, soit, dans l'approximation des petits angles :

D = (a + b/λ²-1)⋅Â

Géométrie

On suppose le prisme placé dans l'air (indice 1). Le rayon incident suit la loi de Snell-Descartes de la réfraction au passage du premier dioptre, donc les angles i et r sont tels que :

(1)

(cf. figure 2).

De même, à la sortie du second dioptre :

(2)

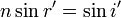
La géométrie impose par ailleurs les relations :

A = r + r′ (3)

et

D = i + i′ - A (4)

À partir de ces relations, un calcul simple dans l'approximation des petits angles permet de déterminer l'ordre de grandeur de l'angle de déviation :

sin i ≃i ; sin i′ ≃ i′ ; sin r ≃r ; sin r′ ≃ r′

soit

i ≃ n⋅r d'après ()

i′ ≃ n⋅r′ d'après ()

l'équation () devient donc

D = n⋅(r + r′) - A

soit d'après ()

D = (n-1)⋅A

l'angle A étant en radian. Dans l'approximation des petits angles, la déviation est indépendante de l'angle d'incidence.

Si on ne peut pas faire l'approximation des petits angles, la déviation est :

Le minimum de déviation

On constate expérimentalement l'existence d'un minimum de la valeur de D lorsqu'on fait varier l'angle d'incidence. On note D_m ce minimum de déviation.

Le principe du retour inverse de la lumière montre alors simplement que la configuration pour ce minimum est nécessairement symétrique. Ceci a donc lieu quand

i = i′,

r = r′.

Des relations précédentes on déduit facilement que ce minimum dépend de l'indice et de l'angle du prisme A :

n⋅sin(A/2) = sin((A + D_m)/2)

Réciproquement, on peut dire que le minimum de déviation dépend de l'indice. Celui-ci n'ayant pas la même valeur selon les composantes monochromatiques, on peut utiliser le prisme comme élément dispersif pour faire de la spectroscopie. Le prisme est alors placé dans un goniomètre.

Conditions d'émergence

Suivant l'angle du prisme, suivant son indice, un rayon arrivant sous une incidence trop faible peut ne pas émerger par la face opposée : il est réfléchi par le dioptre et émerge donc par la base du prisme.

Pour qu'un rayon émerge du prisme il faut que l'angle d'incidence i soit compris entre i_o et 90° :

i_o = arcsin [n⋅sin(Â - arcsin 1/n)]

avec

•  : angle du prisme ;
• n : indice de réfraction