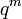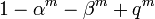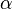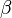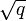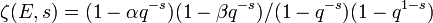Conjectures de Weil - Définition

Introduction

En mathématiques, les conjectures de Weil, qui sont devenues des théorèmes en 1974, ont été des propositions très influentes à la fin des années 1940 énoncées par André Weil sur les fonctions génératrices (connues sous le nom de fonctions zêta locales) déduites du décompte de nombre de points des variétés algébriques sur les corps finis.

Une variété V sur un corps fini à q éléments possède un nombre fini de points sur le corps lui-même, et sur chaque corps fini à éléments contenant ce corps. La fonction génératrice possède des coefficients dérivés des nombres de points sur le corps (essentiellement unique) à éléments.

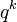
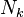
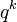
La tâche principale était que ces fonctions zêta devaient être des fonctions rationnelles, devant satisfaire une forme d'équation fonctionnelle, et devaient avoir leurs zéros dans des endroits restreints. Les deux dernières parties étaient tout à fait consciemment modélisées sur la fonction zêta de Riemann et l'hypothèse de Riemann.

Arrière-plan et histoire

En fait, le cas des courbes sur les corps finis a été démontré par Weil lui-même, achevant le projet démarré par le théorème de Hasse sur les courbes elliptiques sur les corps finis. Les conjectures étaient suffisamment naturelles dans une direction, simplement en proposant que les bonnes propriétés connues seraient étendues. Leur intérêt était suffisamment évident dans la théorie des nombres : elles impliquaient l'existence d'un mécanisme qui fournirait les limites supérieures pour les sommes exponentielles, un élément de base dans la théorie analytique des nombres.

Ce que était réellement attirant, à partir du point de vue d'autres domaines mathématiques, était la connexion proposée avec la topologie algébrique. Étant donné que les corps finis sont discrets par nature, et que la topologie parle seulement du continu, la formulation détaillée de Weil (basée sur l'élaboration de quelques exemples) était frappante et novatrice. Il suggérait que la géométrie sur les corps finis devait s'ajuster dans des motifs bien connus se reliant aux nombres de Betti, au théorème du point fixé de Lefschetz et ainsi de suite.

Weil lui-même n'essaya jamais sérieusement de démontrer les conjectures. L'analogie avec la topologie suggérait que la nouvelle théorie homologique serait conçue en s'appliquant dans la géométrie algébrique. Ceci prit deux décennies (ce fut l'objectif central du travail et de l'école d'Alexandre Grothendieck) pour l'élaborer sur les suggestions initiales de Serre et d'autres. La partie rationnelle des conjectures fut démontrée d'abord, par Bernard Dwork en 1960, en utilisant les méthodes p-adiques. Le reste attendit la construction de la cohomologie étale, une théorie dont la définition est relativement profonde. Les démonstrations furent complétées par Pierre Deligne en 1974, en utilisant un argument d'induction sur la dimension, en parlant grossièrement.

Les conjectures de Weil ont, par conséquent, pris leurs places dans la théorie générale (des fonctions L, au sens large). Puisque la cohomologie étale possède plusieurs autres applications, ce développement donne des exemples entre les conjectures (basées sur les exemples et l'intuition), la construction de la théorie, la résolution de problème, et d'avantages inattendus, même dans les parties les plus abstraites des mathématiques pures.

Exemples

Hypersurfaces diagonales

Dans le cas de la fonction f(X,Y,Z) = Xⁿ + Yⁿ + Zⁿ le nombre de solutions dans l'espace affine est donné par:

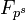
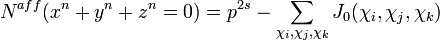
où et χ_i,χ_j,χ_k des caractères additifs no triviaux de tels que χ_iχ_jχ_k = 1. Le nombre de solutions dans l'espace projectif que l'on notera N_s est alors

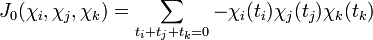
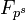
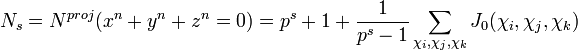
de plus on a:

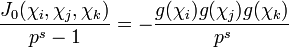
d'où

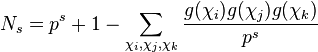
On utilise de plus la relation de Hasse-Davenport pour obtenir cette expression de N_s:

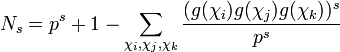
qui implique la rationalité de la fonction zêta associé à l'équation Xⁿ + Yⁿ + Zⁿ car la fonction zêta est une fraction rationnelle si et seulement si:

.

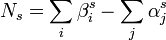
La droite projective

L'exemple le plus simple (autre qu'un point) consiste à prendre X comme étant la droite projective. Le nombre de points de X sur un corps fini à éléments est simplement (où le "+ 1" provient du "point à l'infini"). La fonction zêta est simplement . Il est facile de vérifier toutes les parties des conjectures de Weil directement.

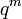
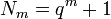
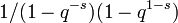
L'espace projectif

Il n'est pas plus difficile de prendre un espace projectif à n dimensions. Le nombre de points de X sur un corps à éléments est simplement . La fonction zêta est simplement

.

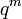
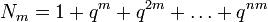
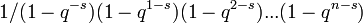
Il est de nouveau facile de vérifier toutes les parties des conjectures de Weil directement.

La raison pour laquelle la droite projective et l'espace projectif étaient si faciles est qu'ils peuvent être écrits comme des unions disjointes d'un nombre fini de copies d'espaces affines, qui rendent le nombre de points sur eux particulièrement facile à calculer. Il est aussi facile de démontrer les conjectures de Weil pour d'autres espaces, tels que les Grassmanniens, qui ont la même propriété.

Les courbes elliptiques

Celles-ci donnent les premiers cas non-triviaux des conjectures de Weil (démontrés par Hasse). Si E est une courbe elliptique sur un corps fini à q éléments, alors le nombre de points de E défini sur le corps à éléments est , où et sont des conjugués complexes de valeur absolue . La fonction zêta est