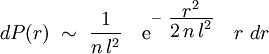Marche aléatoire - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
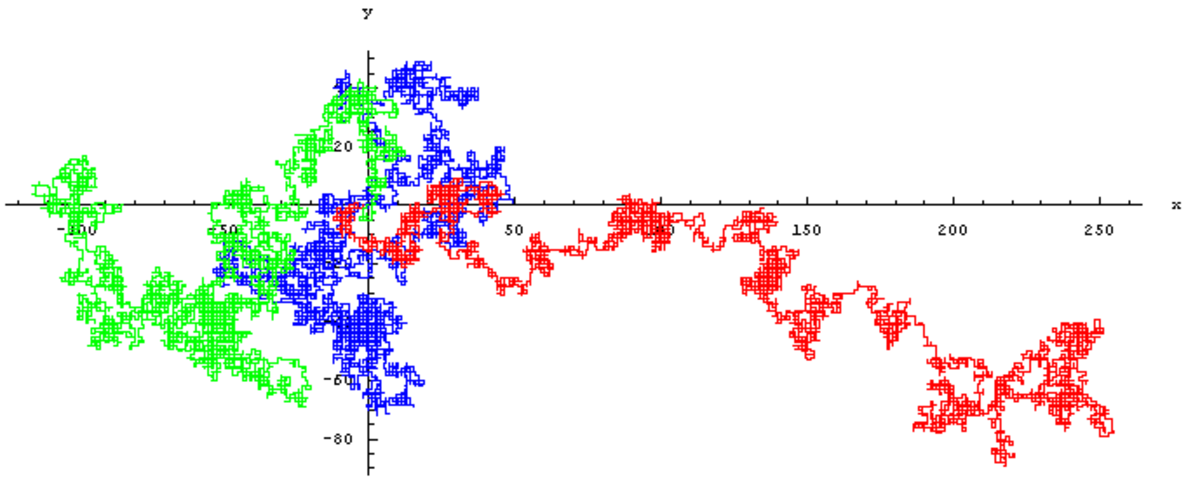
En mathématiques, en économie, et en physique théorique, une marche au hasard est un modèle mathématique d'un système possédant une dynamique discrète composée d'une succession de pas aléatoires, ou effectués « au hasard ». On emploie également fréquemment les expressions marche aléatoire, promenade aléatoire ou random walk en anglais. Ces pas aléatoires sont de plus totalement décorrélés les uns des autres ; cette dernière propriété, fondamentale, est appelée caractère markovien du processus, du nom du mathématicien Markov. Elle signifie intuitivement qu'à chaque instant, le futur du système dépend de son état présent, mais pas de son passé, même le plus proche. Autrement dit, le système « perd la mémoire » à mesure qu'il évolue dans le temps. Pour cette raison, une marche aléatoire est parfois aussi appelée « marche de l'ivrogne ».
Cette modélisation mathématique permet de rendre compte de certains phénomènes naturels, dont l'exemple le plus fameux est le mouvement brownien, correspondant aux mouvements en apparence aléatoires des particules présentes dans le fluide intérieur d'un grain de pollen.
En mathématiques ou en informatique, on étudie souvent des marches au hasard sur des réseaux réguliers ou sur des graphes plus complexes. C'est par exemple la méthode utilisée par le moteur de recherche Google pour parcourir, identifier et classer les pages du réseau internet.
Techniquement, les marches aléatoires sont du domaine de la théorie des probabilités. Une marche aléatoire est en effet un processus stochastique du type chaîne de Markov. Elle se décompose en unités élémentaires appelées pas, dont la longueur peut être elle-même constante, aléatoire ou fixée par le réseau ou le graphe sur lequel on circule. À chaque pas, on a donc un éventail de possibilités pour choisir au hasard la direction et la grandeur du pas. Cet éventail de possibilités peut être discret (choix parmi un nombre fini de valeurs), ou continu.
Historique
L'idée de marche aléatoire a été introduite (sans le nom) en 1905 par le biostatisticien Karl Pearson pour rendre compte des migrations d'une population de moustiques dans une forêt. Pearson y pose la question suivante :
« Un homme part d'un point O et parcours l yards (0,914 m) en ligne droite ; il tourne d'un angle quelconque, et marche de nouveau l yards en ligne droite. Il répète ce processus n fois. Je demande la probabilité qu'après n de ces trajets, il soit à une distance située entre r et r + dr de son point de départ. »
La réponse à cette question est fournie une semaine plus tard par Lord Rayleigh dans la livraison suivante de Nature : lorsque n est suffisamment grand, cette probabilité vaut :
Si Rayleigh fournit si rapidement la réponse, c'est qu'il a lui-même étudié en 1880 un problème connexe : le comportement d'une superposition d'ondes acoustiques toutes de même amplitude, mais de phases aléatoires. Pearson répond à Rayleigh le 10 août :
« J'aurais dû le savoir, mais mes lectures ces dernières années se sont déplacées vers d'autres centres d'intérêt, et on ne s'attend pas à trouver la première étape d'un problème de biométrie dans un mémoire sur l'acoustique. »
Pearson poursuit ensuite :
L'expression « marche aléatoire » n'a été introduite que vers 1919-1921 par le mathématicien hongrois George Pólya, qui utilisait le mot allemand « Irrfahrt ».