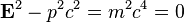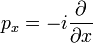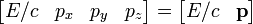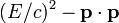Quantité de mouvement - Définition
La liste des auteurs de cet article est disponible ici.
En mécanique quantique
En mécanique quantique, la quantité de mouvement est définie en tant qu'opérateur agissant sur la fonction d'onde. La quantité de mouvement dans la direction x, pour une particule sans charge électrique et sans spin, vaut (en utilisant les unités naturelles
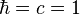
et donc le vecteur
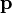
-
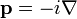
Le principe d'incertitude d'Heisenberg impose une limite à la précision avec laquelle la quantité de mouvement et la position d'un système observable simple peuvent être simultanément connus.
En mécanique relativiste
La quantité de mouvement est une grandeur conservée lors de transformations de translation. Sinon, cela impliquerait une modification sans cause de la position du centre de gravité d'un système de deux corps élastiques qui se percutent.
Aussi, lorsqu'Albert Einstein formula sa théorie de la relativité restreinte, il adapta la définition de la quantité de mouvement afin que celle-ci soit également conservée lors de transformations relativistes. La grandeur ainsi obtenue s'appelle un quadri-moment, c'est une grandeur vectorielle à quatre dimensions qui combine la quantité de mouvement classique et l'énergie :
où
-
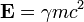
-
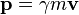
-
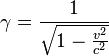
-

La norme de ce quadrivecteur est la grandeur qui reste invariante lors d'une transformation de Lorentz (un changement relativiste de référentiel) :
Les objets de masse nulle, tels que les photons, possèdent aussi un 4-moment où la pseudo-norme du quadri-vecteur p est nulle. On a dans ce cas :
-