Régression de Cox - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La Régression de Cox (modèle à hasard proportionnel) - nommée ainsi d'après le statisticien Britannique David Cox- est une classe de modèles de survie (en) en statistiques. Les modèles de survie étudient le temps écoulé avant qu'un événement ne survienne. Historiquement, dans le modèle de Cox, cet événement est le décès de l'individu, c'est pourquoi on parle généralement de survie et de décès. Au cours des années, l'utilisation du modèle s'est étendue à d'autres situations, l'événement peut donc être de quelconque nature : il peut s'agir de la récidive d'une maladie, ou à l'inverse d'une guérison. D'un point de vue statistique, la nature de l'événement n'est bien-sûr pas importante, il s'agira alors d'interpréter les coefficients en conséquence.
Prenons le cas d'une étude longitudinale, bien souvent, il n'est pas envisageable de suivre les individus sur une longue période, et les événements ne sont pas forcément observés sur toute la population, on parle alors de données censurées (en). L'avantage d'un modèle comme celui de Cox est que l'on peut prendre en compte ces données même si elles ne sont pas "complètes".
Théorie
Le modèle de Cox exprime la fonction de risque instantané de décès λ (on peut aussi trouver les appellations suivantes : fonction de hasard, taux de panne, taux de fiabilité, force de mortalité, taux de hasard...) en fonction du temps t et des covariables
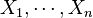
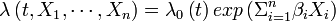
De manière plus formelle, pour un individu, la fonction
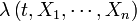
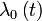
On peut noter quelques points :
- On peut séparer la formule en deux parties, la première (
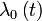
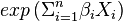
- On dit que le modèle de Cox est semi-paramétrique. En effet, on ne cherche pas à estimer la fonction
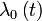
- Il découle de cette formule une hypothèse essentielle du modèle de Cox : celle des risques proportionnels. Pour comprendre cette notion, prenons deux individus j1 et j2 qui ne diffèrent que par une seule covariable, disons la k-ième. On peut imaginer que cette covariable vaut 0 chez j1 et 1 chez j2.
On alors, quel que soit t :
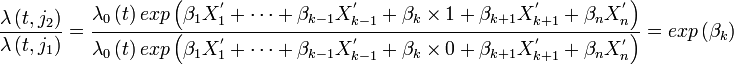
Le rapport est donc indépendant du temps, autrement dit, quel que soit le temps t, l'individu j2 a un risque instantané de mourir exp(βk) fois celui de l'individu j2.
Hypothèse des risques proportionnels
Il s'agit d'une hypothèse forte du modèle de Cox, il faut donc au préalable vérifier que celle-ci est satisfaite. Pour chaque covariable, on teste alors si son effet est indépendant du temps. Cet effet doit être constant, ce qui signifie qu'il peut être bénéfique, nocif ou simplement nul. Il existe différentes méthodes pour vérifier si l'hypothèse des risques proportionnels est satisfaite. On peut s'appuyer sur des méthodes graphiques, par exemple, si l'on veut vérifier l'hypothèse des risques proportionnel sur une covariable Xk -qui prend les valeurs 0 ou 1-, alors on peut regarder si les courbes
![\log\left[-\log\left[S\left(t\right)\right]\right]](https://static.techno-science.net/illustration/Definitions/autres/8/8b7c144bb93692daf58697fbee90af32_b62f4bc42c1859404497016421d86ba7.png)
Il existe cependant des tests statistiques. Parmi eux, le test des résidus de Schoenfeld : pour chaque date de mort ti, on calcule la différence entre les caractéristiques de l’individu décédé (en cas d’ex-aequo, on calcule un résidu pour chaque individu et chaque temps de décès et on somme les résidus) et une moyenne pondérée des caractéristiques des individus à risque de décéder au temps ti. Ceci donne :
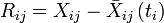
Avec :
- Rij : résidu au temps ti
- Xij : valeur de la covariable j pour l'individu décédé au temps ti
-
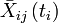
On utilise les résidus standardisés qui sont en fait les résidus divisés par leur variance.
Si l’hypothèse des risque proportionnels est vérifiée, alors les résidus doivent être distribués de la même manière au cours du temps. En plus de la statistique de test, il est courant d’effectuer une représentation graphique des résidus en fonction du temps.
Généralement, cette hypothèse est vérifiée pour la plupart des covariables. Si ce n'est pas le cas, une des solutions est de stratifier sur les covariables qui ne vérifient pas l'hypothèse des risques proportionnels.
Estimations des coefficients
L'estimation des
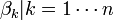
Prenons donc un échantillon de données indépendantes avec les notations suivantes :
- Xi le vecteur colonne des covariables de la i-ème personne (pouvant d'ailleurs dépendre du temps)
- β le vecteur colonne des coefficients βi
-
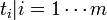
- di le nombre de décès au temps ti
- Di l'ensemble des décès au temps ti
- ri le nombre d'individus à risque de mourir au temps
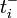
- Ri l'ensemble des individus à risque de mourir au temps
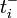
Au temps ti, la probabilité qu’un sujet k décède est :
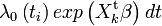
Au temps ti, la vraisemblance de l'ensemble des individus appartenant à Di s'écrit alors :
![\frac{exp\left(\beta^{\operatorname t}\right)^{\Sigma_{k\in D_i}X_k}}{\left[\Sigma_{l\in R_i}exp\left(\beta^{\operatorname t}X_l\right)\right]^{d_i}}](https://static.techno-science.net/illustration/Definitions/autres/1/19443770d44692cd4fe0b6a8e87695c7_3795a7a502bd5371b2ad77d785da7e4e.png)
Finalement, la fonction de vraisemblance (partielle) de Cox peut s'écrire :
Il s’agit donc de résoudre l’équation de sorte que
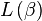
Interprétation des coefficients
Prenons une covariable Xk qui peut prendre deux valeurs : 0 si l'individu prend le traitement A ou 1 s'il s'agit du traitement B. Prenons comme référence les individus qui prennent le traitement A (la manière de procéder pour le codage des variables est parfaitement identique aux modèles tels que la régression logistique ou linéaire), alors le coefficient βk est le Risque Relatif (ici risque instantané de décès) associé au traitement B par rapport au traitement A. Autrement dit, les individus prenant le traitement B ont un risque instantané de décès


















































