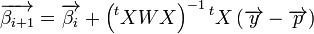Introduction

La régression logistique est une technique statistique qui a pour objectif, à partir d’un fichier d’observations, de produire un modèle permettant de prédire les valeurs prises par une variable catégorielle, le plus souvent binaire, à partir d’une série de variables explicatives continues et/ou binaires.

La régression logistique est largement répandue dans de nombreux domaines. On peut citer de façon non-exhaustive :

• En médecine, elle permet par exemple de trouver les facteurs qui caractérisent un groupe de sujets malades par rapport à des sujets sains.
• Dans le domaine des assurances, elle permet de cibler une fraction de la clientèle qui sera sensible à une police d’assurance sur tel ou tel risque particulier.
• Dans le domaine bancaire, pour détecter les groupes à risque lors de la souscription d’un crédit.
• En économétrie, pour expliquer une variable discrète. Par exemple, les intentions de vote aux élections.

Le succès de la régression logistique repose notamment sur les nombreux outils qui permettent d’interpréter de manière approfondie les résultats obtenus.

Par rapport aux techniques connues en régression, notamment la régression linéaire, la régression logistique se distingue essentiellement par le fait que la variable expliquée est catégorielle.

En tant que méthode de prédiction pour variable catégorielle, la régression logistique est tout à fait comparable aux techniques supervisées proposées en apprentissage automatique (arbre de décision, réseaux de neurones, etc.), ou encore l’analyse discriminante prédictive en statistique exploratoire. Il est notamment possible de les mettre en concurrence pour choisir le modèle le plus adapté pour un problème de prédiction à résoudre.

Notations, hypothèses et estimations

Notations

Dans ce qui suit, nous noterons Y la variable à prédire (variable expliquée), X = (X₁,X₂,...,X_J) les variables prédictives (variables explicatives).

Dans le cadre de la régression logistique binaire, la variable Y prend deux modalités possibles {1,0}. Les variables X_j sont exclusivement continues ou binaires.

• Pour effectuer l'estimation, nous disposons d'un échantillon Ω d'effectif n. Nous notons n₁ (resp. n₀) les observations correspondants à la modalité 1 (resp. 0) de Y.

• P(Y = 1) (resp. P(Y = 0)) est la probabilité a priori pour que Y = 1 (resp. Y = 0). Pour simplifier, nous écrirons p(1) (resp. p(0)).

• p(X / 1) (resp. p(X / 0)) est la distribution conditionnelle des X sachant la valeur prise par Y

• Enfin, la probabilité a posteriori d'obtenir la modalité 1 de Y (resp. 0) sachant la valeur prise par Xest représentée par p(1 / X) (resp. p(0 / X)).

Hypothèse fondamentale

La régression logistique repose sur l’hypothèse fondamentale suivante

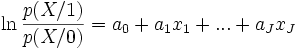
Une vaste classe de distributions répondent à cette spécification, la distribution multinormale déjà vue en analyse discriminante linéaire par exemple, mais également d’autres distributions, notamment celles où les variables explicatives sont booléennes (0/1).

Par rapport à l’analyse discriminante toujours, ce ne sont plus les densités conditionnelles p(X / 1) et p(X / 0) qui sont modélisées mais le rapport de ces densités. La restriction introduite par l'hypothèse est moins forte.

Le modèle LOGIT

La spécification ci-dessus peut être écrite de manière différente. On désigne par le terme LOGIT de p(1 / X) l’expression suivante

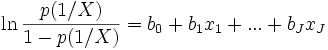
• Il s’agit bien d’une « régression » car on veut montrer une relation de dépendance entre une variable à expliquer et une série de variables explicatives.
• Il s’agit d’une régression « logistique » car la loi de probabilité est modélisée à partir d’une loi logistique.

En effet, après transformation de l’équation ci-dessus, nous obtenons

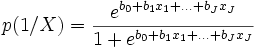
Remarque : Equivalence des expressions

Nous sommes partis de deux expressions différentes pour aboutir au modèle logistique. Nous observons ici la concordance entre les coefficients a_j et b_j. Reprenons le LOGIT

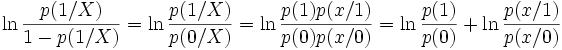
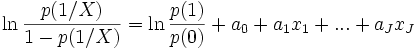
Nous constatons que

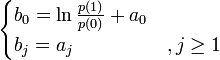
Estimation — Principe du maximum de vraisemblance

A partir d’un fichier de données, nous devons estimer les coefficients b_j de la fonction LOGIT. Il est très rare de disposer pour chaque combinaison possible des , même si ces variables sont toutes binaires, de suffisamment d’observations pour disposer d’une estimation fiable des probabilités P(1 / X) et P(0 / X). La méthode des moindres carrés ordinaire est exclue. La solution passe par une autre approche : la maximisation de la vraisemblance.

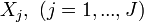
La probabilité d’appartenance d’un individu ω à un groupe, que nous pouvons également voir comme une contribution à la vraisemblance, peut être décrit de la manière suivante

La vraisemblance d’un échantillon Ω s’écrit alors :

Les paramètres qui maximisent cette quantité sont les estimateurs du maximum de vraisemblance de la régression logistique.

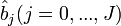
L’estimation dans la pratique

Dans la pratique, les logiciels utilisent une procédure approchée pour obtenir une solution satisfaisante de la maximisation ci-dessus. Ce qui explique d’ailleurs pourquoi ils ne fournissent pas toujours des coefficients strictement identiques. Les résultats dépendent de l’algorithme utilisé et de la précision adoptée lors du paramétrage du calcul.

Dans ce qui suit, nous notons le vecteur des paramètres à estimer. La procédure la plus connue est la méthode Newton-Raphson qui est une méthode itérative du gradient (voir Algorithme d'optimisation). Elle s’appuie sur la relation suivante :

• est la solution courante à l'étape . est une initialisation possible ;
• est le vecteur des dérivées partielles premières de la vraisemblance ;
• est la matrice des dérivées partielles secondes de la vraisemblance ;
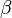
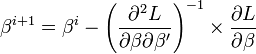
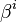
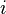
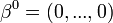
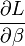
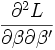
• les itérations sont interrompues lorsque la différence entre deux vecteurs de solutions successifs est négligeable.

Cette dernière matrice, dite matrice hessienne, est intéressante car son inverse représente l’estimation de la matrice de variance co-variance de . Elle sera mise en contribution dans les différents tests d’hypothèses pour évaluer la significativité des coefficients.

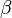
Sous forme matricielle :

Évaluation