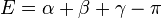Résolution d'un triangle - Définition

Introduction

En géométrie, la résolution d'un triangle consiste en la détermination des différents éléments d'un triangle (longueurs des côtés, mesure des angles, aire) à partir de certains autres. Historiquement, la résolution des triangles fut motivée

• en cartographie, pour la mesure des distances par triangulation ;
• en géométrie euclidienne chez les grecs, pour la résolution de nombreux problèmes de géométrie.
• en navigation, pour le point, qui utilise des calculs de coordonnées terrestres et astronomiques (trigonométrie sphérique).

Aujourd'hui, la résolution des triangles continue d'être utilisée dans un grand nombre de problèmes faisant intervenir la triangulation (architecture, relevés cadastraux, vision binoculaire) et, plus généralement, la trigonométrie (astronomie, cartographie).

En géométrie euclidienne, la donnée de trois des éléments du triangles, dont au moins un côté, est nécessaire et suffisante à la résolution du triangle, l'un des cas de résolution pouvant admettre deux solutions. En géométrie sphérique ou hyperbolique, la donnée des trois angles est également suffisante. La résolution fait intervenir la trigonométrie, en particulier certaines relations classiques dans le triangle comme le théorème d'Al-Kashi, la loi des sinus, la loi des tangentes, et la somme de ses angles.

Cas de résolution en géométrie sphérique

La résolution d'un triangle en géométrie sphérique (géométrie non-euclidienne) est légèrement différente du cas euclidien, car la loi des sinus ne permet pas d'obtenir un côté de manière univoque — uniquement son sinus. De plus, un triangle sphérique dont les trois angles sont connus est soluble, contrairement à un triangle du plan euclidien et la solution est unique.

Les formules utilisées pour résoudre un triangle sphérique sont :

• les généralisations du théorème d'Al-Kashi (variantes portant sur les angles et sur les côtés) ;
• le théorème de l'Huilier ;
• les analogies de Napier ;
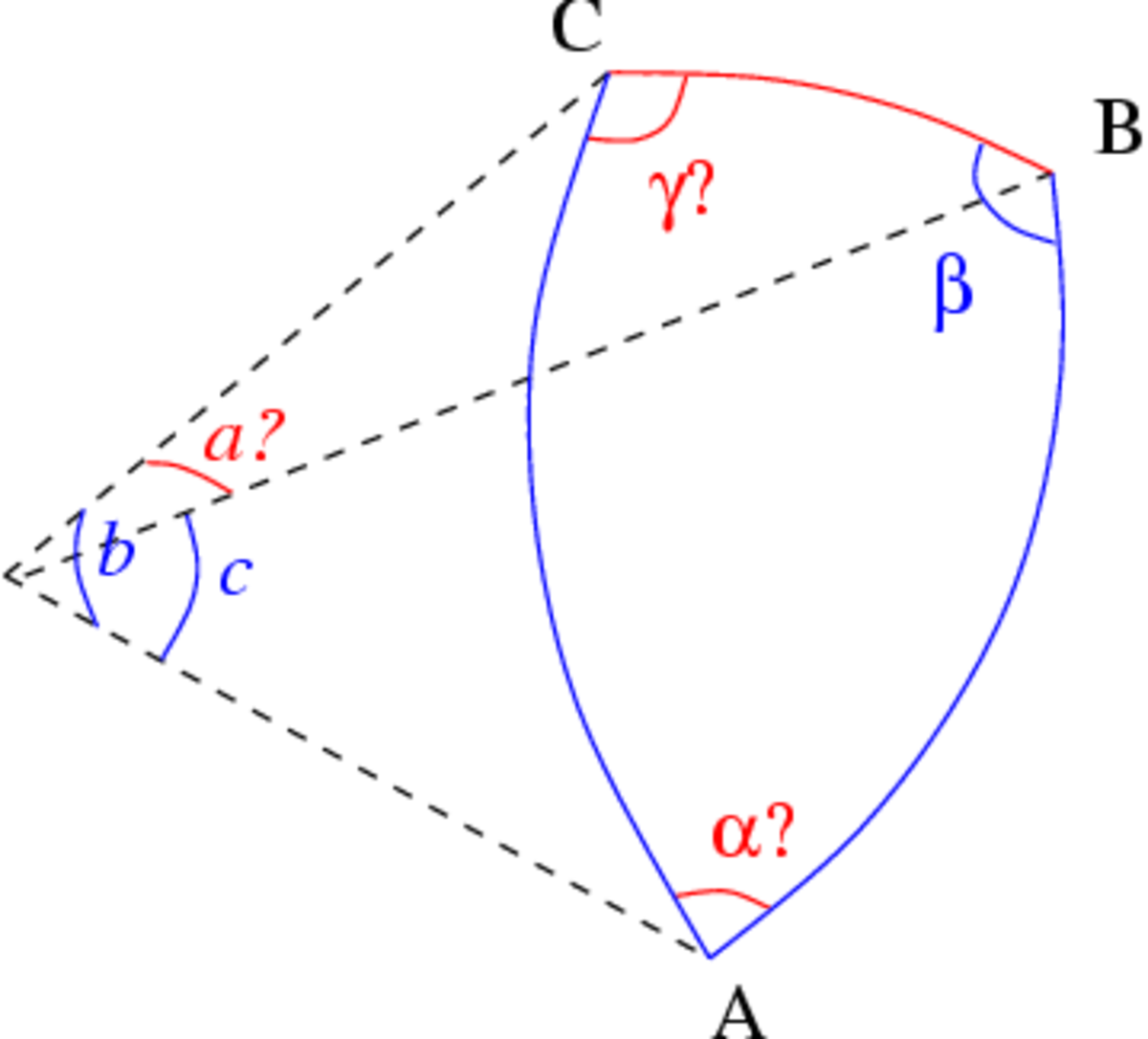
• la somme des angles d'un triangle vaut π plus l'excès E (=S/R²).

Les trois côtés

Dans un triangle dont les trois côtés a, b et c sont connus, les angles s'obtiennent par la généralisation du théorème d'Al-Kashi et l'aire par le théorème de l'Huilier :

• ,
• ,
• ,
• où .

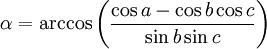
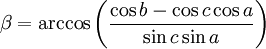
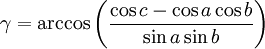
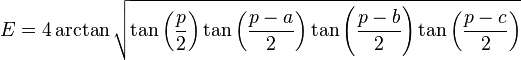
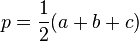
Un angle et les deux côtés adjacents

Dans un triangle où deux côtés a et b et l'angle qu'ils forment γ sont connus, le dernier côté s'obtient par le théorème d'Al-Kashi généralisé et les deux angles restants par les analogies de Napier :

• ,
• ,
• ,
• .

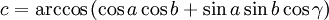
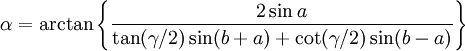
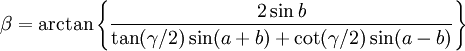
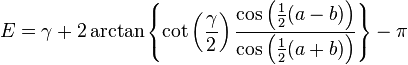
Un angle, le côté opposé et un côté adjacent

On considère un triangle dont un angle β, un côté adjacent c et le côté opposé b sont connus. L'angle γ s'obtient par la loi des sinus et les éléments restants par les analogies de Napier. Il n'y a de solution que si

.

Alors

• ,
• ,
• .
• 

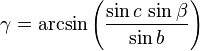
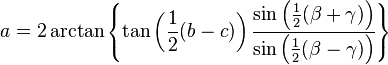
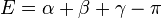
Une autre solution existe lorsque b > c et que γ est aigu :

• , etc.

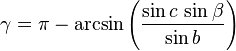
Deux angles et le côté commun

Dans un triangle où deux angles α et β sont connus, ainsi que le côté commun à ces angles c, le dernier angle s'obtient par la formule d'al-Kashi et les deux derniers côtés par les analogies de Napier. Les formules pour l'angle manquant et les côtés ressemblent à celles du cas de résolution complémentaire () :

• ,
• ,
• ,
• .

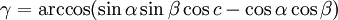
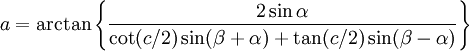
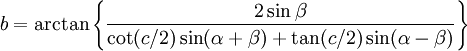
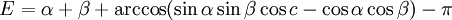
Deux angles et un côté non commun

On considère un triangle dans lequel deux angles α et β sont connus, ainsi qu'un côté opposé à l'un de ces angles a. Le côté b se trouve par la loi des sinus et les éléments restants par les analogies de Napier. On notera la similitude entre les équations ci-dessous et le cas de résolution complémentaire () :

• ,
• ,
• ,
• .

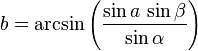
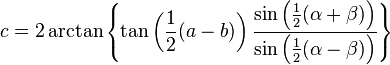
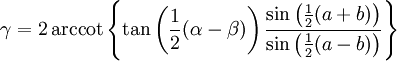
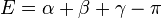
Si a est aigu et que α > β, il existe une autre solution :

• , etc.

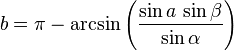
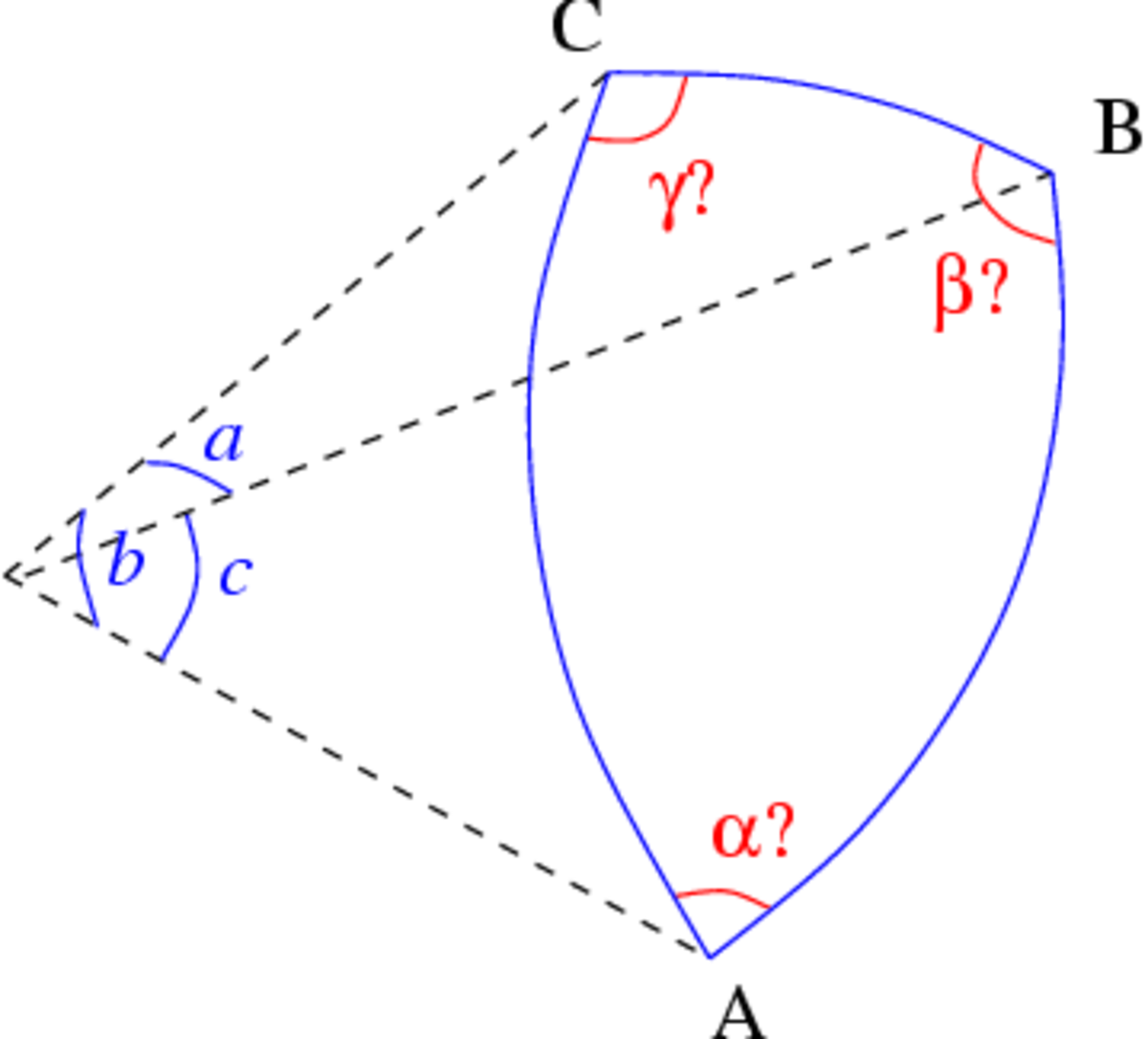
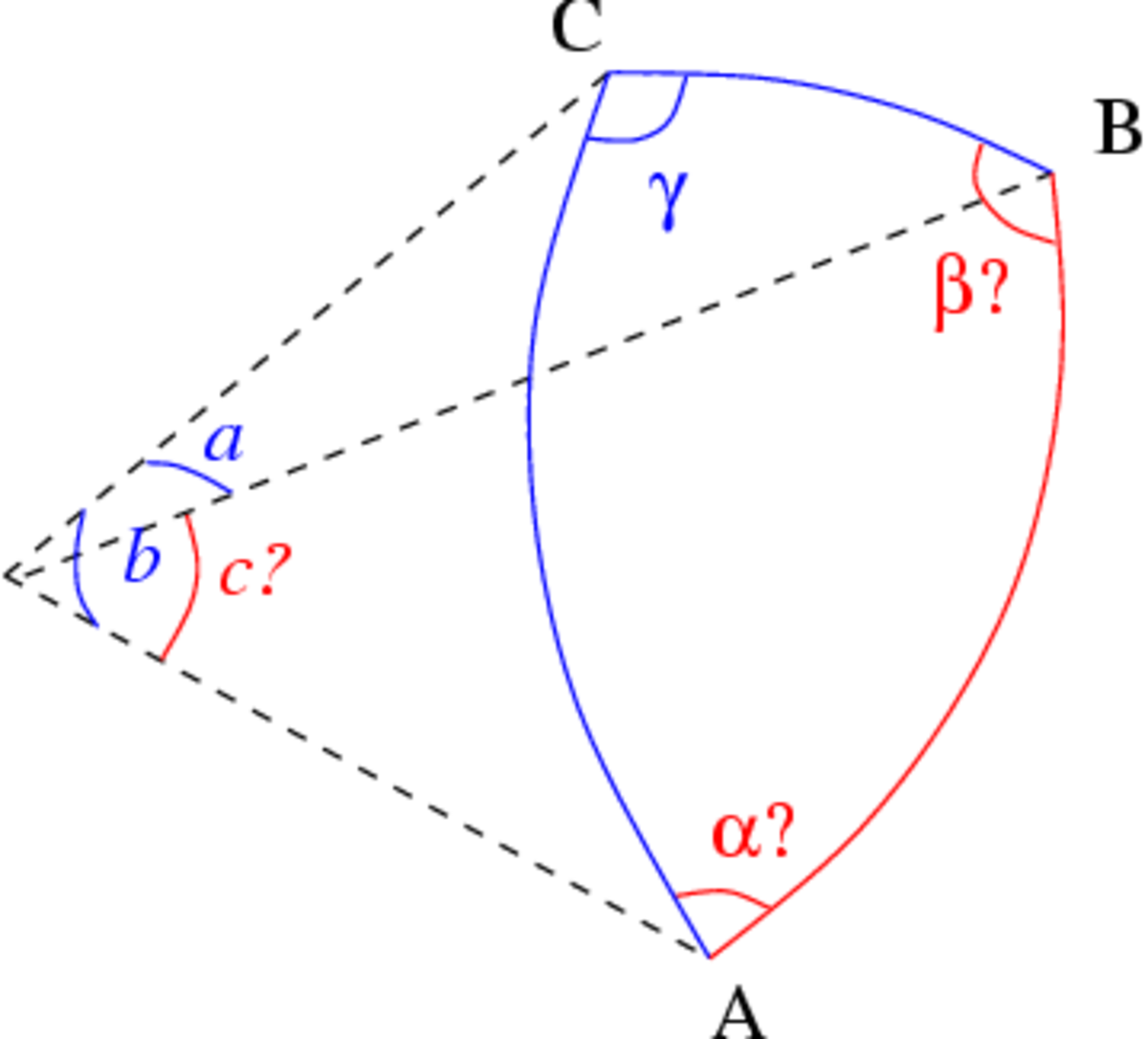
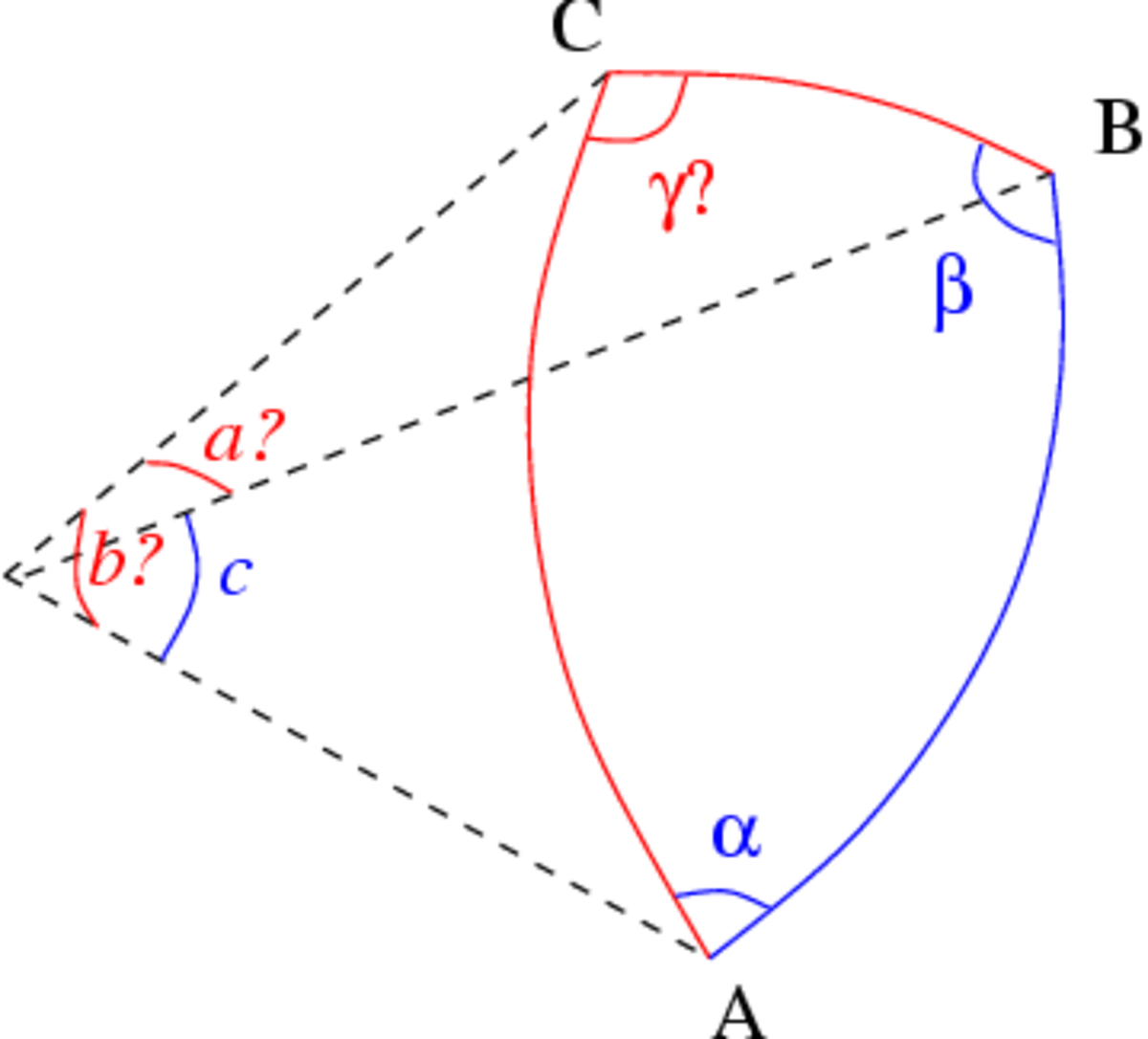
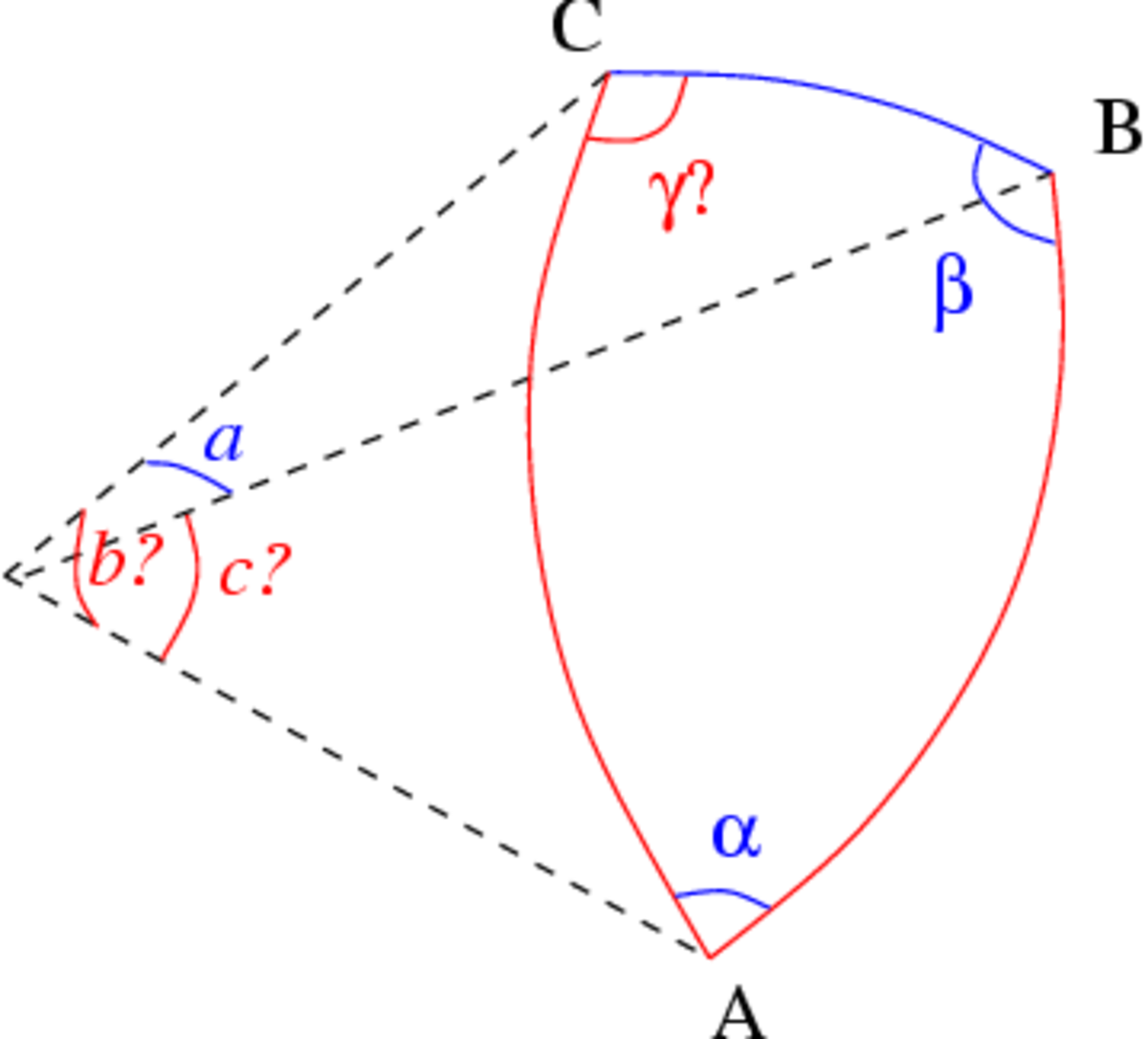
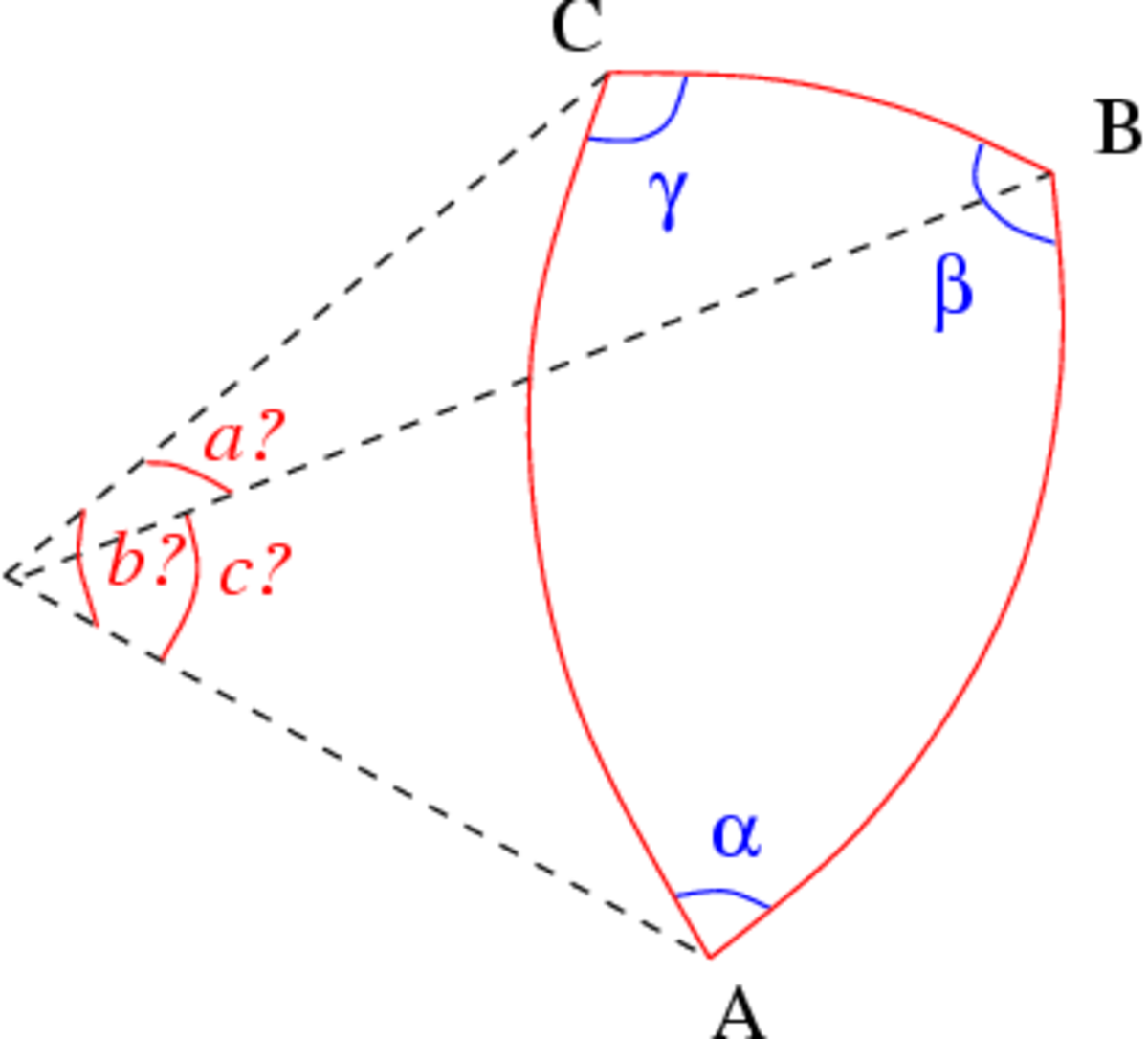
Les trois angles

Dans le cas où les trois angles sont connus, les côtés s'obtiennent par une variante du théorème d'Al-Kashi pour les angles. Les formules donnant les côtés sont semblables à celles du cas de résolution complémentaire () :

• ,
• ,
• .
•
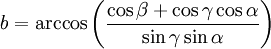
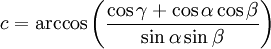