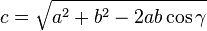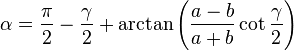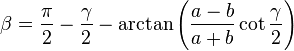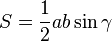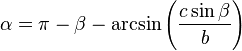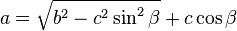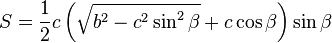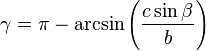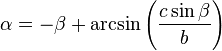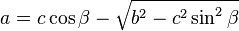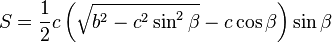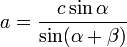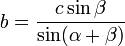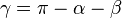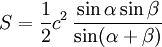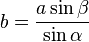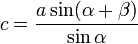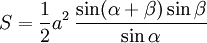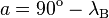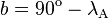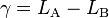Résolution d'un triangle - Définition

Cas de résolution en géométrie euclidienne

La résolution d'un triangle en géométrie euclidienne utilise un certain nombre de relations entre éléments du triangle. Les plus souvent utilisées sont

• le théorème d'Al-Kashi ;
• la formule de Héron ;
• la loi des sinus ;
• la loi des tangentes ;
• la somme des angles d'un triangle vaut π rad soit 180 °,

bien qu'il soit également possible d'utiliser d'autres relations pour aboutir à une solution.

Ci-dessous sont listés les différents cas de figure en fonction des trois éléments connus parmi les trois angles et les trois côtés. Les formules analytiques sont données pour les côtés et/ou les angles inconnus, ainsi que l'aire S. Elles doivent être adaptées pour une détermination numérique car, prises telles quelles, elles donnent des erreurs importantes pour les triangles « en épingle », c'est-à-dire dont un des côtés est petit par rapport aux autres et les triangles « presque rectangles », c'est-à-dire dont un des angles fait environ 90°.

Les trois côtés

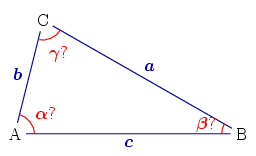
On considère un triangle dont les trois côtés a, b et c sont connus. Les angles sont déduits à partir du théorème d'Al-Kashi et l'aire, de la formule de Héron :

• 
• 
• 
• , avec

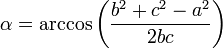
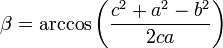
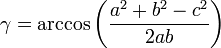
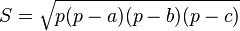
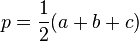
Un angle et les deux côtés adjacents

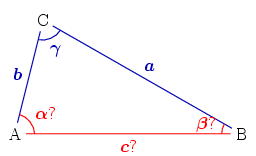
On considère un triangle dont l'angle γ est connu, ainsi que les deux côtés adjacents a et b. Le dernier côté s'obtient grâce au théorème d'Al-Kashi, les deux angles manquants par la loi des tangentes et le complément à π, et l'aire par la formule du produit vectoriel :

• 
• 
• 
• 

Un angle, le côté opposé et un côté adjacent

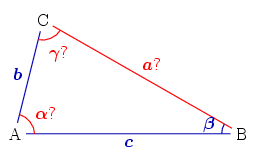
On considère un triangle dont un angle β est connu, ainsi qu'un côté adjacent de cet angle c et le côté opposé b. Le deuxième angle γ s'obtient par la loi des sinus, le dernier angle α par complément à π et le dernier côté par la loi des sinus :

• 
• 
• 
• 

Si β est aigu et que b < c, il existe une seconde solution :

• 
• 
• 
• 

La résolution n'est pas possible pour toutes les valeurs des paramètres et que la condition suivante doit être réalisée :

.

Deux angles et le côté commun

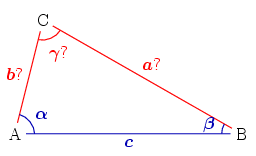
On considère un triangle dont un côté c et les deux angles α et β qui le bordent sont connus. Le dernier angle s'obtient par complément à π et les deux autres côtés par la loi des sinus :

• 
• 
• 
• 

Deux angles et un côté non commun

On considère un triangle dont deux angles α et β sont connus, ainsi qu'un côté non commun à ces deux angles a. Le dernier angle s'obtient par complément à π et les deux autres côtés par la loi des sinus :

• 
• 
• 
• 

Exemples d'application

Triangulation

Voir l'article détaillé Triangulation.

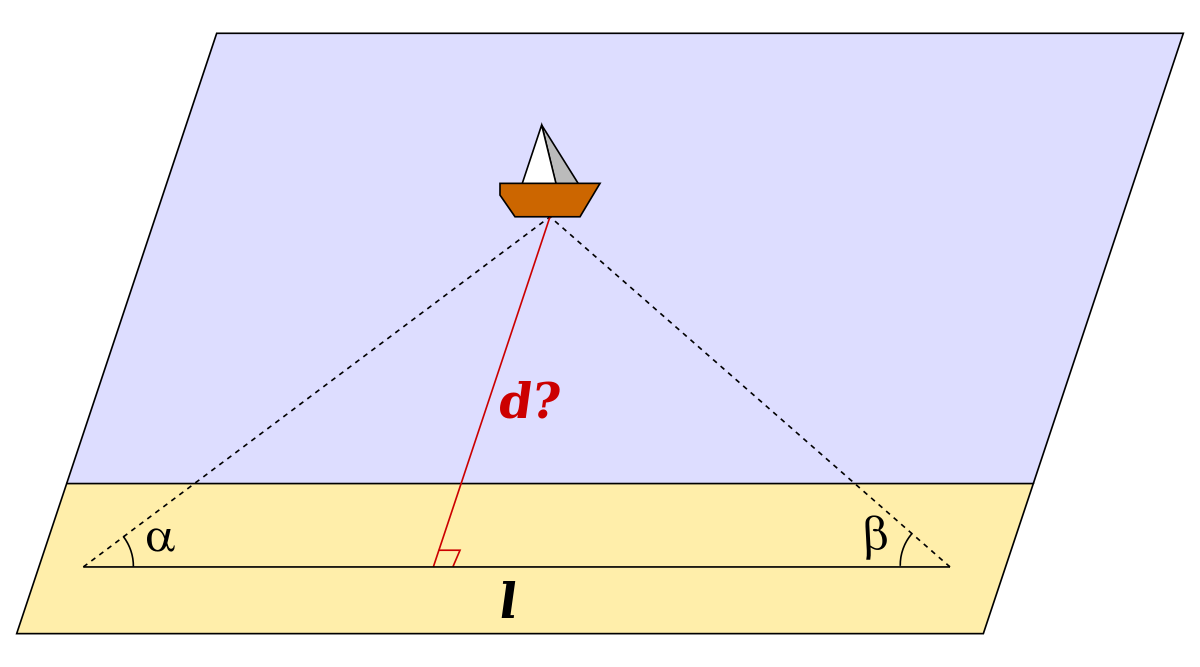
La figure 1 ci-contre indique une méthode de détermination de la distance d'un bateau par triangulation : de deux points dont on connaît la distance l, on mesure sa direction, que ce soit l'azimut à l'aide d'une boussole, ou les angles α et β avec la ligne joignant les deux points. Les mesures effectuées, il est possible d'en déduire la distance graphiquement en reportant les éléments connus sur un graphique avec une échelle idoine. Une formule analytique peut être par ailleurs trouvée en résolvant le  :

.

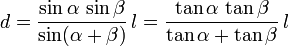
Une variante est utilisée en navigation côtière : les angles sont estimés grâce aux azimuts des amers (points de référence sur terre) vus depuis le navire.

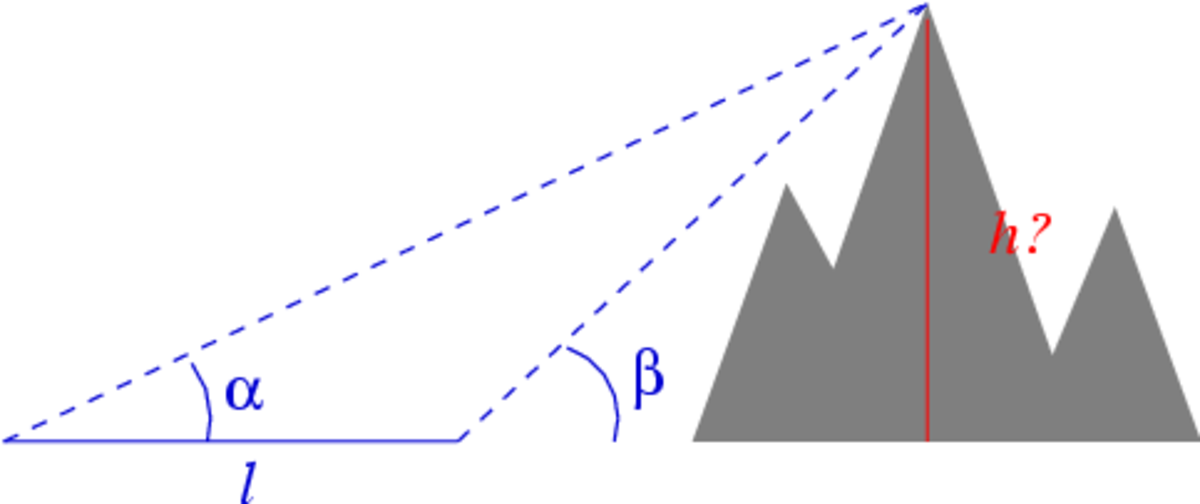
Une autre possibilité est la mesure de la hauteur h d'une colline ou d'une montagne depuis une vallée en mesurant sa hauteur angulaire α et β en deux points de distance connue l. La figure 2 ci-contre donne un cas simplifié dans lequel les points de mesure et la projection du sommet sur le sol sont alignés. La hauteur de la montagne peut être déterminée graphiquement ou bien analytiquement par résolution du triangle () :

.

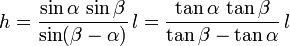
Dans la pratique la méthode de résolution se heurte à quelques difficultés : le terrain n'est pas forcément plat, ce qui nécessite un estimation de la pente entre les deux points ; le sommet réel n'est pas forcément observable depuis la plaine et le point le plus haut tel qu'observé varie de position entre les deux points d'observation par effet de tangence ; les différents éléments du relief doivent être triangulés de proche en proche à partir des côtes ce qui accumule les erreurs de mesure. Ainsi, la cartographie par satellite a modifié de plusieurs mètres les valeurs traditionnelles estimées de certains sommets. Malgré ces difficultés, au XIX^e siècle, Friedrich Georg Wilhelm von Struve a fait construire l'arc géodésique de Struve, une chaîne de repères géodésiques traversant l'Europe sur 2800 km de la Norvège à la Mer Noire et dont le but était de mesurer la taille et la forme de la terre : en 1853, le scientifique obtient une mesure du méridien terrestre à 188 m près (2×10^-5) et de l'aplatissement de la terre à 1% près.

Distance entre deux points du globe

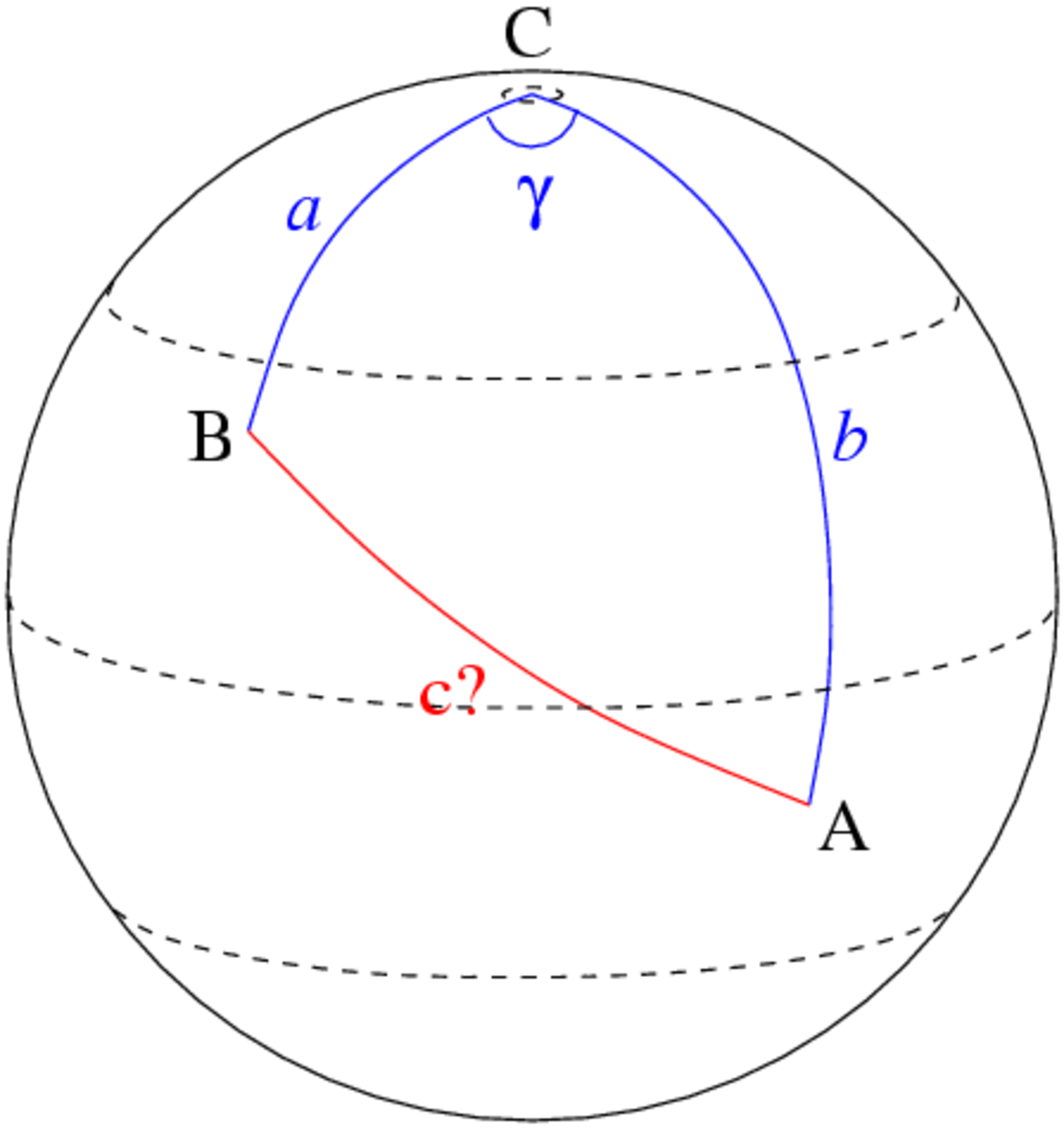
On considère deux points du globe A et B de latitudes respectives λ_A et λ_B, et de longitudes L_A et L_B. Pour déterminer leur distance on considère le triangle ABC, où C est le pôle nord. Dans ce triangle sont connus :

• 
• 
• 

La résolution du triangle dans le permet de conclure que

,

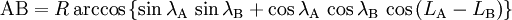
où R est le rayon de la terre. Les coordonnées doivent être converties en radians pour une application numérique, à moins que la calculatrice accepte les degrés dans les fonctions trigonométriques.