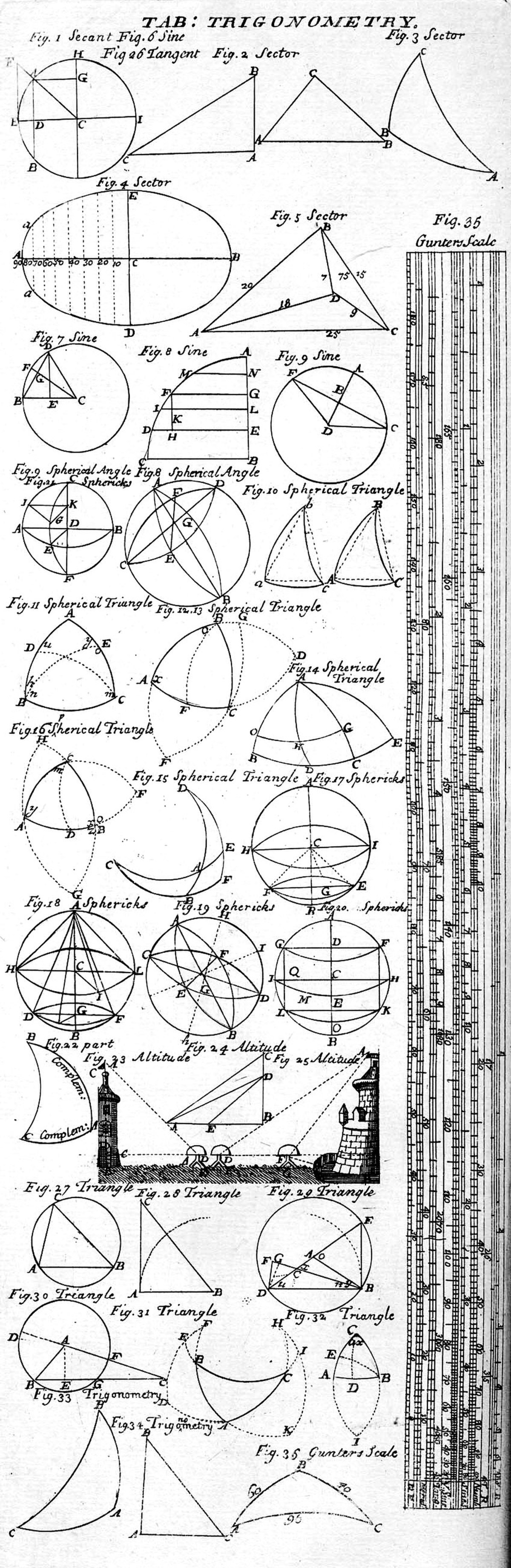
Trigonométrie - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La trigonométrie (du grec τρίγωνος / trígonos, « triangulaire », et μέτρον / métron, « mesure ») est une branche des mathématiques qui traite des relations entre distances et angles dans les triangles et des fonctions trigonométriques telles que sinus, cosinus et tangente.
Présentation
Histoire de la trigonométrie
Premières techniques de mesure du triangle
Les origines de la trigonométrie remontent aux civilisations d'Égypte antique, de Mésopotamie et de la vallée de l'Indus, il y a plus de 4000 ans. Il semblerait que les Babyloniens aient basé la trigonométrie sur un système numérique à base 60. Lagadha (-1350 ; -1200) est le premier mathématicien à utiliser la géométrie et la trigonométrie pour l'astronomie. La plupart de ses travaux sont aujourd'hui détruits.
La première utilisation de sinus apparaît dans les sulba Sutras en Inde, entre 800 et 500 avant J.C., où le sinus de π/4 (45°) est correctement calculé comme 1/√2 dans un problème de construction d'un cercle de même aire qu'un carré donné (le contraire de la quadrature du cercle).
Les astronomes grecs
L'astronome et mathématicien grec Hipparque de Nicée (-190 ; -120) construisit les premières tables trigonométriques sous la forme de tables de cordes : elles faisaient correspondre à chaque valeur de l'angle au centre (avec une division du cercle en 360°), la longueur de la corde interceptée dans le cercle, pour un rayon fixe donné. Ce calcul correspond au double du sinus de l'angle moitié, et donne donc, d'une certaine façon, ce que nous appelons aujourd'hui une table de sinus. Toutefois, les tables d'Hipparque n'étant pas parvenues jusqu'à nous, elles ne nous sont connues que par le grec Ptolémée, qui les publia, vers l'an 150, avec leur mode de construction dans son Almageste. C'est ainsi qu'elles furent redécouvertes à la fin du Moyen Âge par Georg von Purbach et son élève Regiomontanus. On attribue à Ménélaüs d'Alexandrie (fin du Ier siècle) des développements en trigonométrie sphérique, au moins partiellement présents dans l'Almageste et longtemps attribués à Ptolémée lui-même.
Le mathématicien indien Aryabhata, en 499, donne une table des sinus et des cosinus. Il utilise zya pour sinus, kotizya pour cosinus et otkram zya pour l'inverse du sinus. Il introduit aussi le sinus verse.
Un autre mathématicien indien, Brahmagupta, utilise en 628 l'interpolation numérique pour calculer la valeur des sinus jusqu'au second ordre.
Essor dans le monde musulman
Omar Khayyam (1048-1131) combine l'utilisation de la trigonométrie et la théorie de l'approximation pour fournir des méthodes de résolutions d'équations algébriques par la géométrie. Des méthodes détaillées de constructions de tables de sinus et cosinus pour tous les angles sont écrites par le mathématicien Bhaskara en 1150. Il développe aussi la trigonométrie sphérique. Au XIIIe siècle, Nasir al-Din Tusi, à la suite de Bhaskara, est probablement un des premiers à considérer la trigonométrie comme une discipline distincte des mathématiques. Enfin, au XIVe siècle, Al-Kashi réalise des tables de fonctions trigonométriques lors de ses études en astronomie.
En Europe : redécouverte de Ptolémée
En Europe, la trigonométrie se développe vers le milieu du XIVe siècle avec la traduction en latin des œuvres de Ptolémée. Les pionniers en ce domaine sont Georg von Purbach et surtout son étudiant Regiomontanus. Suivent au début du XVIe siècle les traités d'Oronce Finé, Pedro Nunes et Joachim Rheticus. Le mathématicien silésien Bartholomäus Pitiscus publie un travail remarquable sur la trigonométrie en 1595, dont le titre (Trigonometria) a donné son nom à la discipline. C'est le mathématicien flamand Adrien Romain qui introduit la notation moderne
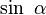
Applications
Les applications de la trigonométrie sont immenses. En particulier, elle est utilisée en astronomie avec la technique de triangulation qui permet de mesurer la distance entre les étoiles. Les autres champs où la trigonométrie intervient (liste non exhaustive) : acoustique, optique, électronique, statistiques, économie, biologie, chimie, médecine, physique, météorologie, géodésie, géographie, cartographie, cryptographie, etc.