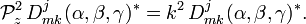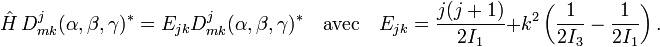Rotateur rigide - Définition
La liste des auteurs de cet article est disponible ici.
Rotateur rigide à forme arbitraire
Un rotateur rigide à forme arbitraire est un corps rigide de forme arbitraire à centre de masse fixe (ou se mouvant de manière uniforme et rectiligne) dans un espace
En spectroscopie microonde - spectroscopie basée sur les transitions rotationnelles - on classe habituellement les molécules (perçues comme rotateurs rigides) de la manière suivante :
- rotateurs sphériques
- rotateurs symétriques
- rotateurs symétriques oblates (aplatis)
- rotateurs symétriques prolates (allongés)
- rotateurs asymétriques
Cette classification dépend des valeurs relatives de leurs moments d'inertie principaux.
Coordonnées du rotateur rigide
Les différentes branches de la physique et de l'ingéniérie utilisent différentes coordonnées pour la description de la cinématique d'un rotateur rigide. En physique moléculaire, on utilise quasi-exclusivement les angles d'Euler. Dans les applications de la mécanique quantique, il est pertinent d'utiliser des angles d'Euler dans une convention qui est une extension simple des conventions des coordonnées sphériques.
La première étape consiste à lier un référentiel orthonormé direct (système tridimensionnel d'axes orthogonaux et normés) au rotateur (référentiel lié). Ce référentiel peut être attaché arbitrairement au corps, mais on peut utiliser également les axes principaux — les vecteurs propres normalisés du tenseur d'inertie, qui peuvent toujours être choisis orthonormaux (le tenseur étant symétrique). Lorsque le rotateur possède un axe de symétrie, celui coïncide habituellement avec l'un des axes principaux. Il est pratique de choisir un référentiel lié dans lequel l'axe z est l'axe de la symétrie d'ordre le plus élevé.
On commence par aligner le référentiel lié avec un référentiel fixe (dit du laboratoire) de telle façon que les axes x, y et z coïncident avec les axes X, Y et Z du référentiel du laboratoire (les axes sont dans les plans adéquats). Puis le solide et son référentiel sont pivotés d'un angle positif
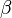
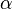
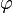
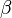
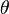
Si le solide ne possède pas de symétrie cylindrique (axiale), une dernière rotation autour de son axe z (avec pour coordonnées polaires
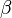
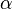
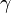
La convention sur les angles d'Euler décrite ici est connue sous le nom de convention z'' − y' − z ; on peut montrer (de manière relativement simple) que c'est équivalent à la convention z − y − z dans laquelle l'ordre des rotations est inversée.
La matrice correspondant aux trois rotations est le produit matriciel :
Soit
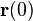
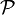
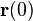
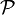
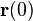
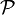
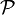
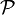
En particulier, si
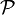
qui montre la correspondance entre les coordonnées sphériques (en convention physique).
La connaissance des angles d'Euler comme fonction du temps t et les coordonnées initiales
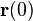
Énergie cinétique classique
On postulera à partir d'ici que le référentiel lié est un référentiel avec les axes principaux. Cela diagonalise le tenseur inertiel instantané
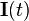
où les angles d'Euler sont dépendant du temps et détermine de fait la dépendance temporelle de
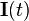
L'énergie cinétique classique T du rotateur rigide peut être exprimée de plusieurs manières :
- en fonction de la vitesse angulaire,
- sous forme lagrangienne
- en fonction du moment angulaire
- sous forme hamiltonienne
Chacune de ces formes possède son utilité et peut être trouvée dans la littérature. On les présente ci-après.
En fonction de la vitesse angulaire
T s'écrit en fonction de la vitesse angulaire :
avec
Le vecteur
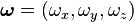
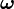
Sous forme lagrangienne
La substitution de
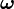
où
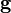
En fonction du moment angulaire
L'énergie cinétique est parfois écrite comme une fonction du moment angulaire
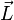

Puisque le référentiel lié se déplace (dans le temps), ces composantes ne sont pas indépendantes du temps. Si l'on considère
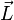
Sous forme hamiltonienne
La forme hamiltonienne de l'énergie cinétique s'écrit en termes de moments généralisés :
où on pose
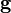
où le tenseur métrique inverse est donné par :
Ce tenseur inverse est nécessaire à l'obtention de l'opérateur de Laplace-Beltrami, qui (multiplié par
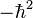
Le hamiltonien classique donné ci-dessus peut être réécrit dans la forme suivante, qui est nécessaire pour l'intégration de phase se produisant dans la mécanique statistique classique des rotateurs rigides,
Le rotateur rigide en mécanique quantique
Comme d'habitude, la quantification est assurée par le remplacement des moments généralisés par des opérateurs donnant les dérivées premières par rapport à ses variables (positions) canoniquement conjuguées. Ainsi,
et de même pour pβ et pγ. Il est à noter que cette loi remplace la fonction des trois angles d'Euler, de leurs dérivées temporelles et des moments d'inertie caractérisant le rotateur rigide, pα relativement complexe, par un simple opérateur différentiel qui ne dépend pas du temps ou des moments d'inertie et qui porte sur un angle d'Euler seulement.
La loi de quantification est suffisante pour obtenir les opérateurs correspondant aux moments angulaires classiques. Il y en a deux types : les opérateurs de moment angulaire liés au référentiel absolu ou liés au référentiel lié au corps rigide. Les deux sont des opérateurs vectoriels, c'est-à-dire que tous les deux possèdent trois composantes qui se transforment les unes en les autres par rotation de leurs référentiels respectifs. La forme explicite des opérateurs de moment angulaire du rotateur rigide est donnée ici (au facteur multiplicatif
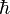
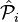
La règle de quantification n'est pas suffisante pour obtenir l'opérateur d'énergie cinétique à partir du hamiltonien classique. Classiquement pβ commutant avec cosβ, sinβ et les inverses de ces fonctions, la position de ces fonctions trigonométriques dans le hamiltonien classique est arbitraire. Après la quantification, la commutation n'est plus permise et l'ordre des opérateurs et fonctions dans le hamiltonien (opérateur d'énergie) devient cruciale. Podolsky indiqua en 1928 que l'opérateur de Laplace-Beltrami (multiplié par
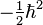
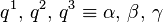
où | g | est le déterminant du tenseur g :
Étant donnée -dessus l'inverse du tenseur métrique, la forme explicite de l'opérateur d'énergie cinétique en termes des angles d'Euler s'ensuit par simple substitution. L'équation aux valeurs propres correspondantes fournit l'équation de Schrödinger pour le rotateur rigide sous la forme qui fut résolue pour la première fois par Kronig et Rabi (pour le cas spécifique du rotateur symétrique). C'est l'un des rares cas pour lesquels l'équation de Schrödinger peut être résolue de manière analytique. Tous ces cas furent résolus dans l'année de la formulation de cette équation.
Il est actuellement habituel de procéder comme il suit. On peut montrer que
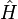
L'action de
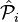
donc l'équation de Schrödinger pour le rotateur sphérique (I = I1 = I2 = I3) est résolue pour l'énergie (2j + 1)2-dégénérée et égale à
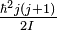
La toupie symétrique (un rotateur symétrique) est caractérisée par I1 = I2. C'est une toupie prolate (en forme de cigare) si I3 < I1 = I2. Dans ce dernier cas, on écrit le hamiltonien :
et on utilise :
Alors,
La valeur propre Ej0 est dégénérée 2j + 1 fois, pour toutes les fonctions propres avec
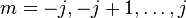
Le problème de la toupie asymétrique (
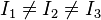
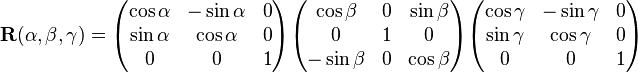
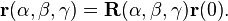
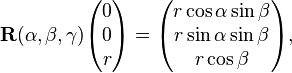
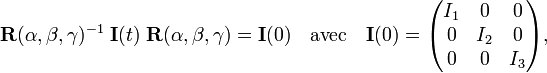
![T = \frac{1}{2} \left[ I_1 \omega_x^2 + I_2 \omega_y^2+ I_3 \omega_z^2 \right]](https://static.techno-science.net/illustration/Definitions/autres/1/1567e4fb259766941584a80d25480f84_ec3517b1d3e66e3b2fd5e78fb3597c8c.png)
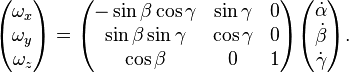
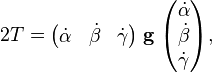
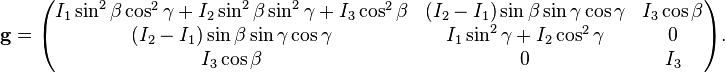
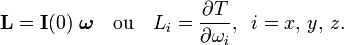
![T = \frac{1}{2} \left[ \frac{L_x^2}{I_1} + \frac{L_y^2}{I_2}+ \frac{L_z^2}{I_3}\right].](https://static.techno-science.net/illustration/Definitions/autres/4/4ac24bebd7c5e648a6763fb6c2d6f6e5_dc5e245e994da22735d1fcd25a0af431.png)
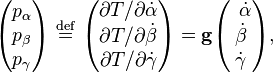
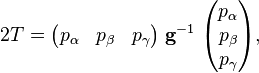
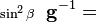
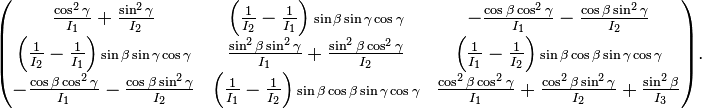
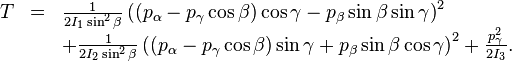
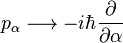
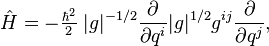
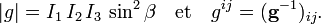
![\hat{H} = \tfrac{1}{2}\left[ \frac{\mathcal{P}_x^2}{I_1}+ \frac{\mathcal{P}_y^2}{I_2}+ \frac{\mathcal{P}_z^2}{I_3} \right].](https://static.techno-science.net/illustration/Definitions/autres/e/ec73bc0a45a9dd954eea9a5917e10bbb_c682c74a9d33a3fb786adb649e8aeb02.png)
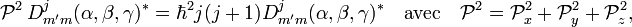
![\hat{H} = \tfrac{1}{2}\left[ \frac{\mathcal{P}^2}{I_1}+ \mathcal{P}_z^2\Big(\frac{1}{I_3} -\frac{1}{I_1} \Big) \right],](https://static.techno-science.net/illustration/Definitions/autres/d/dc81bcf96fa8ab7774408255881d49a7_9f4d442ec79423e2b72b4ab5e4114e72.png)