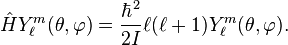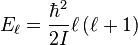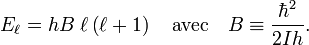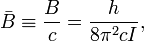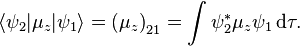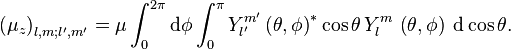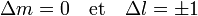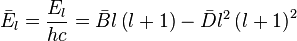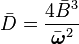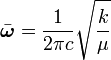Rotateur rigide - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
Le rotateur rigide est un modèle mécanique utilisé pour expliquer les systèmes en rotation (et particulièrement en mécanique quantique). Un rotateur rigide quelconque est un objet tridimensionnel rigide, comme par exemple une toupie. Afin d'orienter un tel objet dans l'espace, trois angles sont nécessaires. Le rotateur linéaire, objet bidimensionnel, est un cas particulier de rotateur rigide en trois dimensions ne nécessitant que deux angles pour décrire son orientation. On peut citer comme exemple de rotateur linéaire une molécule diatomique. De manière plus générale, des molécules comme l'eau (rotateur asymétrique), l'ammoniac (rotateur symétrique) ou le méthane (rotateur sphérique) sont tridimensionnels (se référer à la classification des molécules).
Rotateur linéaire
Le modèle du rotateur rigide linéaire consiste en deux masses ponctuelles situées à distances fixées de leur centre de masse. La distance fixe entre les deux masses et les mesures des masses sont les seules caractéristiques du modèle rigide. Cependant, pour de nombreux systèmes diatomiques réels ce modèle est trop simpliste, les distances interatomiques n'étant pas immuables. Des corrections au modèle rigide peuvent être effectuées afin de compenser les petites variations de distances. Cependant, même dans ce cas de figure le modèle du rotateur rigide reste un bon point de départ comme modèle d'ordre zéro.
Rotateur linéaire rigide classique
Le rotateur linéaire classique consiste en deux masses pontuelles m1 et m2 (avec pour masse réduite
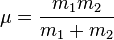

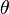

où
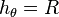
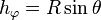
Les facteurs d'échelles sont importants dans les applications de mécanique quantique car ils sont présents dans l'expression du laplacien en coordonnées curvilignes. Dans notre cas (R constant) :
Le hamiltonien classique d'un rotateur linéaire rigide est :
Rotateur linéaire rigide quantique
Le modèle du rotateur rigide peut être utilisé en mécanique quantique afin de prédire l'énergie de rotation d'une molécule diatomique. L'énergie de rotation dépend du moment d'inertie du système, I. Dans le référentiel du centre de masse, le moment d'inertie est égal à :
- I = μR2
où μ est la masse réduite de la molécule et R la distance entre les deux atomes.
En mécanique quantique, les niveaux d'énergie d'un système peuvent être déterminés en résolvant l'équation de Schrödinger :
où Y est la fonction d'onde et
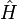
où

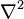
Cet opérateur apparait aussi dans l'équation de Schrödinger de l'atome d'hydrogène après la séparation de la partie radiale. L'équation aux valeurs propres devient :
Le symbole
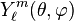
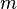
est
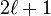
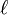
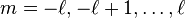
On peut écrire en introduisant la constante de rotation B :
En unité de longueur réciproque, la constante de rotation est :
où c est la vitesse de la lumière. Si les unités CGS sont utilisées pour h, c et I,
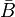
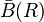
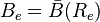
Un spectre de rotation typique consiste en une série de pics correspondant aux transitions entre niveaux avec différentes valeurs de nombre quantique secondaire (
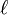
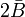
Règles de sélection
Les transitions rotationnelles d'une molécule se produisent quand la molécule absorbe un photon (une particule avec un champ électromagnétique quantifié). Selon l'énergie du photon (c'est-à-dire la longueur d'onde du champ électromagnétique), cette transition peut être aperçue comme une raie satellite d'une transition vibrationnelle et/ou électronique. Les transitions rotationnelles « pures », dans lesquelles la fonction d'onde vibronique (électronique plus vibrationnelle) n'est pas modifiée, se produisent dans la région des micro-ondes du spectre électromagnétique.
Les transitions rotationelles ne peuvent typiquement être observées que quand le nombre quantique secondaire est modifiée d'une unité (
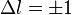
Une transition se produit si cette intégrale est non-nulle. En séparant la partie rotationnelle de la fonction d'onde moléculaire de la partie vibronique, on peut montrer que cela signifie que la molécule doit avoir un moment dipolaire permanent. Après intégration sur les coordonnées vibroniques, la partie rotationnelle suivante du moment de transition reste
Ici
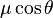
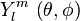
Rotateur linéaire non-rigide
Le rotateur rigide est habituellement utilisé pour décrire l'énergie de rotation de molécules diatomiques mais n'est pas complètement pertinent, en raison de la variation de liaison interatomique (et donc de la distance R). La liaison s'étire lorsque la rotation de la molécule s'accroit (augmentation de la valeur du nombre quantique secondaire l). Cet effet peut être pris en compte en introduisant un facteur de correction connu sous le nom de constante de distortion centrifuge
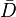
où
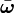
Le rotateur non-rigide est un modèle à la précision acceptable pour les molécules diatomiques mais reste imparfait. Cela est dû au fait que bien que le modèle prenne en compte l'étirement de rotation, il ignore l'étirement de la liaison imputable à l'énergie vibrationnelle (anharmonicité du potentiel).
![2T = \mu R^2\big [\dot{\theta}^2+(\dot\varphi\,\sin\theta)^2\big]= \mu R^2 \big(\dot{\theta}\;\; \dot{\varphi} \Big) \begin{pmatrix} 1 & 0 \\ 0 & \sin^2 \theta \\ \end{pmatrix} \begin{pmatrix} \dot{\theta}\\ \dot{\varphi} \end{pmatrix} = \mu \Big(\dot{\theta}\;\; \dot{\varphi} \Big) \begin{pmatrix} h_\theta^2 & 0 \\ 0 & h_\varphi^2 \\ \end{pmatrix} \begin{pmatrix} \dot{\theta}\\ \dot{\varphi} \end{pmatrix},](https://static.techno-science.net/illustration/Definitions/autres/0/0b95acaf64dd6cae2f0cf2e38dd9a9ed_a037e847832ddf1b6c9e8b66054c6768.png)
![\nabla^2 = \frac{1}{h_\theta h_\varphi}\left[ \frac{\partial}{\partial \theta} \frac{h_\varphi}{h_\theta} \frac{\partial}{\partial \theta} +\frac{\partial}{\partial \varphi} \frac{h_\theta}{h_\varphi} \frac{\partial}{\partial \varphi} \right]= \frac{1}{R^2}\left[\frac{1}{\sin\theta} \frac{\partial}{\partial \theta} \sin\theta \frac{\partial}{\partial \theta} +\frac{1}{\sin^2\theta}\frac{\partial^2}{\partial \varphi^2} \right].](https://static.techno-science.net/illustration/Definitions/autres/f/ff54584fae92d1e5e76c4aa797d306ac_6e0fbf9d040b22ef99dc62c90541a3be.png)
![H = \frac{1}{2\mu R^2}\left[p^2_{\theta} + \frac{p^2_{\varphi}}{\sin^2\theta}\right].](https://static.techno-science.net/illustration/Definitions/autres/d/dc4f5760ed7424d599c8e167dcae4708_ac921cba1abedb6c1afe6c5157473aea.png)
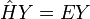
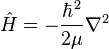
![\hat H =- \frac{\hbar^2}{2I} \left [ {1 \over \sin \theta} {\partial \over \partial \theta} \left ( \sin \theta {\partial \over \partial \theta} \right ) + {1 \over {\sin^2 \theta}} {\partial^2 \over \partial \varphi^2} \right]](https://static.techno-science.net/illustration/Definitions/autres/b/be8462f5e7ae2ea6a44eb9712a08ee87_35c72b3c80ba3062b53f503f39ee178c.png)