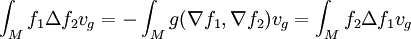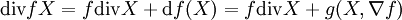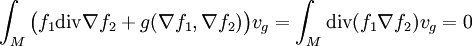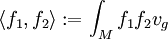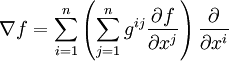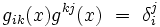Opérateur de Laplace-Beltrami - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
L'opérateur de Laplace-Beltrami est une généralisation de l'opérateur laplacien aux variétés riemanniennes. On part de la définition classique
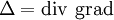
Avertissement : Dans cet article, on utilise la convention de sommation d'Einstein. Même quand le signe somme n'est pas omis, on s'impose la discipline de ne sommer que par rapport à un indice se trouvant à la fois en positions inférieure et supérieure.
Divergence associée à une forme volume
Sur une variété différentielle M orientable, la divergence est naturellement associée à une forme volume. Si ω est une telle forme, toute autre forme de degré maximum s'écrit de façon unique fω, où f est une fonction. Cela s'applique à la dérivée de Lie de ω par rapport à un champ de vecteurs X. La divergence de X (par rapport à ω) est l'unique fonction telle que
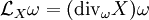
D'après la formule
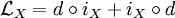
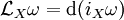
Si ω s'écrit en cordonnées locales
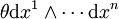
(car
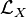
Si
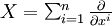
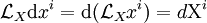
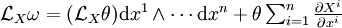
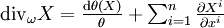
Remarque sur l'orientabilité : L'introduction d'une forme volume suppose la variété orientable. Mais si on change la forme volume ω en son oppposée, divωX) ne change pas. En fait, la divergence ne dépend que de la densité associée à ω. Contrairement aux apparences, l'hypothèse d'orientabilté est inutile, on a en fait utilisé une orientation locale.
L'exemple le plus important est celui de la divergence définie par la forme volume canonique d'une métrique riemannienne.
En coordonnées locales
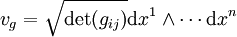
Définition et propriétés de base du laplacien
On définit l'opérateur de Laplace-Beltrami comme l'opérateur différentiel du second ordre
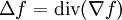
En coordonnées locales,
Si f1 et f2 sont C2 et à support compact on a
Pour le voir, on remarque que si f est une fonction et X un champ de vecteurs,
En appliquant cette relation à f = f1 et
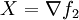
puisque d'après la formule de Stokes l'intégrale de la divergence d'un champ de vecteurs à support compact est nulle.
Cette formule exprime le fait que Δ est un opérateur formellement autoadjoint sur
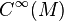
(noter l'analogie avec les opérateurs symétriques en dimension finie.
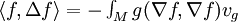
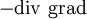

Gradient associé à une métrique riemannienne
Le gradient d'une fonction (disons lisse) f est l'unique champ de vecteurs, noté
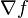
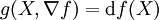
Ici, gij(x) est l'inverse du tenseur métrique, défini en coordonnées par
où
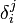
Bibliographie
- Peter Sarnak ; Spectra of hyperbolic surfaces, Bulletin of the American Mathematical Society 40 (2003), 441-478. Texte disponible en ligne.
- Isaac Chavel, Eigenvalues in Riemannian geometry, Academic Press.
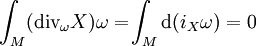
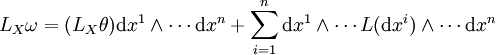
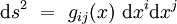
![\Delta \ = \ \frac{1}{\sqrt{g}} \ \partial_{i} \left[ \sqrt{g} g^{ij} \partial_{j} \right]](https://static.techno-science.net/illustration/Definitions/autres/4/414fbc863e514cb776f01d8452bfc667_701a549b0049c2703c7aee76b710825f.png)