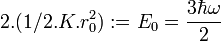Saturation des inégalités d'Heisenberg - Définition
La liste des auteurs de cet article est disponible ici.
Inégalité d'Heisenberg radiale
Afin de pouvoir traiter l'atome d'hydrogène, on va introduire l' inégalité d'Heisenberg radiale, ce qui est relativement moins étudié dans la littérature.
On considère uniquement les états s , à symétrie radiale.
- Soit R l'opérateur tel que R² = X² + Y² + Z² := X1² + X2² + X3², en changeant de notation afin de pouvoir éventuellement généraliser (idem pour P )
Le commutateur de P1 et de R est [P1, R] = -i X1/r ( on a pris
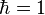
Et donc on reconnaît la dérivation usuelle : [P1,g(R)] = -i (X1/r).g'(R).
- Soit A1 l'opérateur A1 := P1 + k X1.f(R), k réel , f(r) aussi.
Soit N l'opérateur N := A1*. A1 + A2*. A2 + A3*. A3 (parce qu'on pense à la généralisation de l'opérateur nombre de bosons)
Le calcul donne : N = P² +k².r².f(R)² + k (3f(R) + R.f'(R)), opérateur positif pour tout k.
D'où l' inégalité d'Heisenberg radiale pour les états s de symétrie radiale :
, pour toute f(r) réelle.
En saturation, on retrouve bien les résultats précédents de l'oscillateur 3D, en prenant f(r)=1.
Si f(r) = r^k, on trouve :
avec la même limitation qu'en mécanique classique: k > -3.
Application à l'oscillateur 3D
Dans le cas du potentiel 1/2 k (x² + y² + z²), il est clair que la séparation des variables donne immédiatement la fonction d'onde :
![\psi(x,t) = N e^{-[3r^2/4 r_0^2]} e^{-\frac{3 i \omega t}{2}}](https://static.techno-science.net/illustrationWebp/Definitions/autres/7/710902b97aa51679d14685f0025d6e4d_34fa4421167e2197c5f4c71e1179f36d.png)
Compléments sur l'Énergie cinétique radiale
Ce paragraphe se place dans le cadre des précédentes réflexions, où la non-commutativité joue un rôle crucial.
L'opérateur impulsion vaut, d'après Dirac,
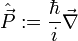
L'opérateur énergie cinétique s'écrit donc :
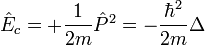
L'habitude est de séparer l'opérateur P² en deux opérateurs quand le champ est central, en faisant intervenir l'opérateur moment cinétique L et l'opérateur impulsion-radiale Pr et il convient d'être très prudent :
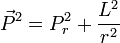
étant précisé que L.P = 0 et L.r = 0 en tant qu'opérateurs.
L'opérateur P²r agit sur une fonction d'onde découplée S(r)/r . f( θ,φ) comme -
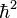
Le calcul de l'opérateur dr/dt est donné par le théorème usuel :
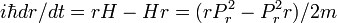
avec
![[r, P_r^2] = 2 i \hbar P_r](https://static.techno-science.net/illustrationWebp/Definitions/autres/4/4991b507f881a7daa5bca205cdbe9e43_96e4704524c1380698dc928e9f00a81b.png)
dr/dt = Pr/m , ce qui est somme toute assez facile à retenir mnémotechniquement.
Si la symétrie radiale est respectée, [L², H] = 0 et dans l'état de moment cinétique l , L² = l(l+1)
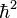
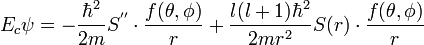
ceci conduira à une équation radiale assez simple à mémoriser ( cf atome d'hydrogène).
Mais il reste à expliquer pourquoi tous les calculs se combinent aussi bien. Et de plus , dans le cas coulombien , expliquer la symétrie SO(4) qui donne le vecteur excentricité. Voir aussi vecteur de Runge-Lenz.
Application à l'atome d'hydrogène
Dans le cas du potentiel V(r) = -e²/r, choisir f(r) = 1/r :
L'inégalité d'Heisenberg saturée s'écrit cette fois:
, en appelant a la moyenne harmonique de R (c’est-à-dire la moyenne de l'opérateur 1/R).
- la valeur de k assurant la saturation est juste k = -
- on en déduit que la fonction d'onde est annihilée par A1 := P1 -
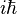
![[\frac{d}{dr} + {1 \over a }]\psi(r)=0](https://static.techno-science.net/illustrationWebp/Definitions/autres/8/8d99d760a139168338c29cd6ae4ac5a6_b9dc186880f0b30b117033dae857aad1.png)
D'où il résulte que
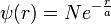
Il s'agit de la fonction d'onde saturée ( naturellement, on vérifie que <1/R> = 1/a) .
- Energie minimale: l'inégalité d'Heisenberg donne aussi:
E =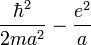 
égalité toujours vraie, pour tout état s.
Cette énergie est minimale quand elle est saturée et que a (moyenne harmonique de r) vaut :
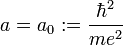
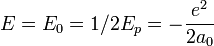
(conformément au théorème du viriel).
On a ainsi trouvé ce que ne pouvait pas donner la théorie de l'atome de Bohr (il y avait inexistence des états s) : la non-commutativité et la saturation de l'inégalité d'Heisenberg sont ainsi inscrits au cœur profond de la Mécanique quantique.
Remarque interrogative : y a-t-il une relation avec le fait que c'est <1/r> qui intervient , et le changement de variable de Binet u(t) = 1/r(t) en mécanique classique ?
note, les états cohérents : Plus généralement, il se trouve souvent que les cas de saturation se retrouvent être des états propres de l'hamiltonien. Il y a beaucoup de liens entre cette remarque anodine et la théorie plus sophistiquée des états cohérents.
