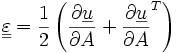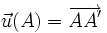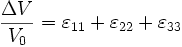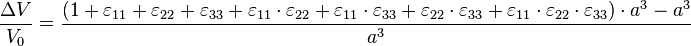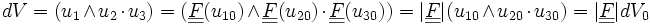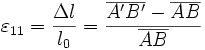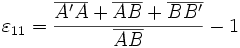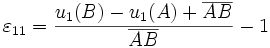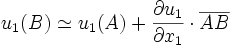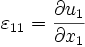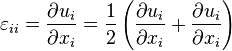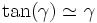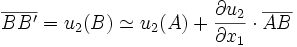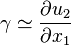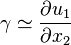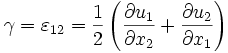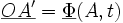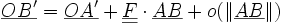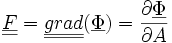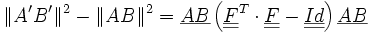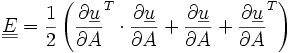Tenseur des déformations - Définition

Introduction

Le tenseur des déformations, est un tenseur symétrique d'ordre 2 servant à décrire l'état de déformation local résultant de contraintes (efforts internes).

L'état de déformation d'un solide est décrit par un champ de tenseur, c'est-à-dire que le tenseur des déformations est défini en tout point du solide. On parle de ce fait de champ de déformation.

Les composantes sont notées ε_ij, avec :

• les termes diagonaux ε_ii sont les allongements relatifs dans la direction i (selon l'axe x_i) ;
• les autres termes ε_ij (i ≠ j) sont les γ, les demies variations de l'angle droit (en supposant un petit volume de matière cubique avant déformation).

Dans le cadre de l'élasticité linéaire, le tenseur des déformations est relié au champ de contrainte par la loi de Hooke généralisée.

Champ de déplacement

Dans le cas de petites déformations, ce tenseur est le tenseur de Green, un tenseur dérivé du champ de déplacement.

Soit A un point du solide au repos ; après déformation, il devient le point A' . On appelle déplacement du point A le vecteur

On peut relier le tenseur des déformations au champ de déplacement :

(Opérateur des déformations linéarisé).

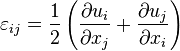
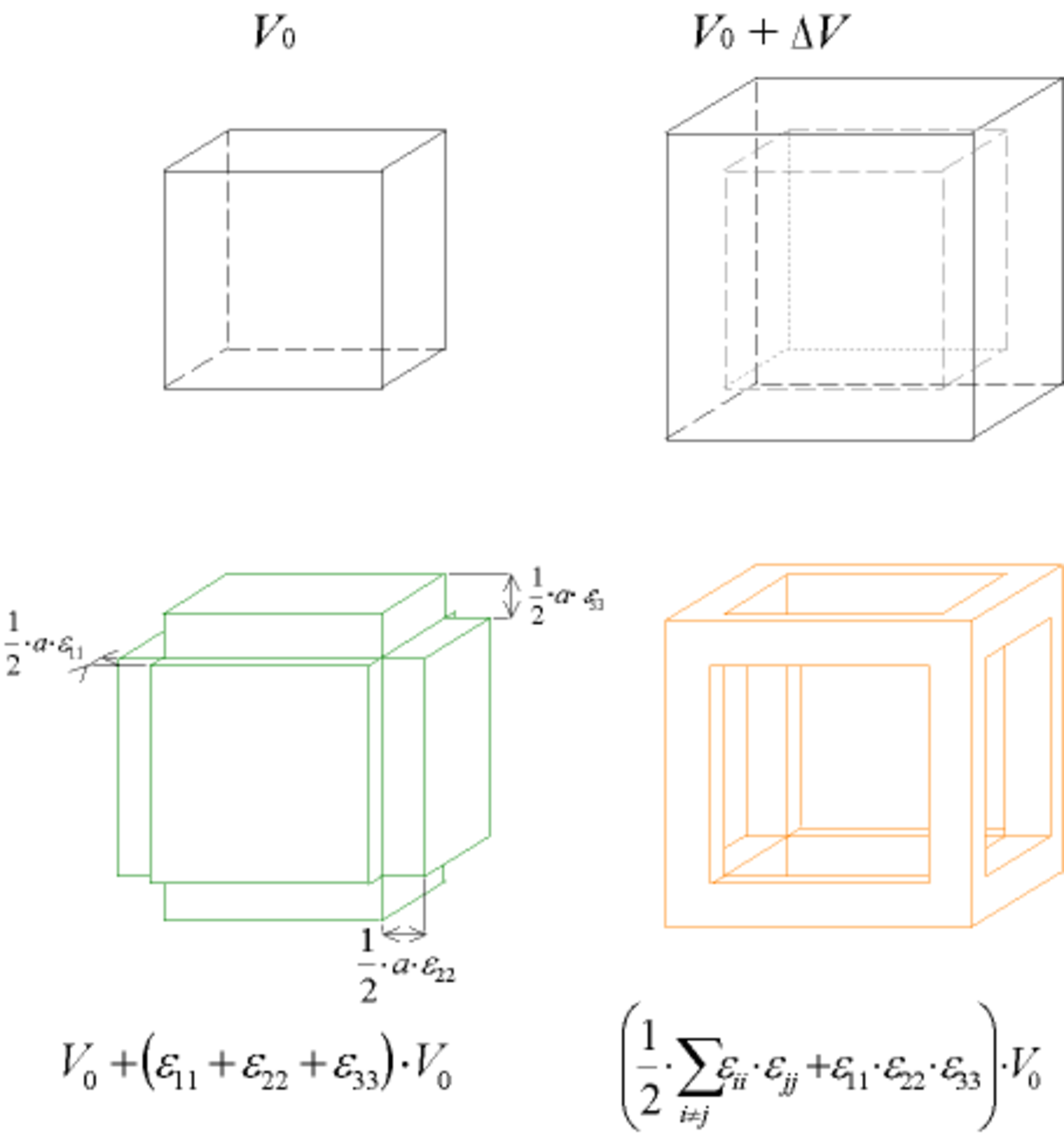
Variation de volume relative

La variation de volume relative ΔV/V₀ est la trace du tenseur :

En effet, si l'on considère un cube d'arrête a, après déformation on a un quasi-cube (les variations d'angle ne changent pas le volume) de dimension et V₀ = a³, soit

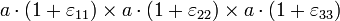
comme on est en très faible déformation,

1 >> ε_ii >> ε_ii·ε_jj >> ε₁₁·ε₂₂·ε₃₃

d'où le résultat.

On en déduit que dans le cas du cisaillement pur, il n'y a pas de variation de volume.

De manière plus rigoureuse, la variation de volume relative ΔV/V₀ est égale à |F|-1.

En effet, soit le prisme de Ω₀ élémentaire engendré par (u₁₀,u₂₀,u₃₀). Sa transformée par Φ est le prisme engendré par (u₁,u₂,u₃).

Soit dV le volume de la transformée, et dV₀ celui du prisme initial.

On a

d'où ΔV/V= |F|-1

Définition de l'opérateur des déformations

Allongement uni-dimensionnel

Prenons le cas d'un segment [AB], parallèle à l'axe x₁, devenant le segment [A'B' ], la déformation étant également parallèle à x₁.

La déformation ε₁₁ vaut (exprimée en distances algébriques) :

Sachant que

et

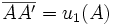
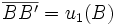
la déformation vaut donc

Si l'on se place en petites déformations, on peut faire le développement limité du premier ordre de u₁ :

et ainsi

De manière plus générale :

Cisaillement pur

Considérons maintenant du cisaillement pur. Un carré ABCD, où [AB] est parallèle à x₁ et [AD] est parallèle à x₂, se transforme en un losange AB'C'D' , symétrique selon la première bissectrice du plan.

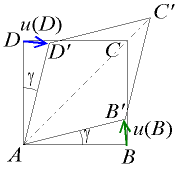
La tangente de l'angle γ vaut :

.

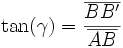
Pour les petites déformations, on a

ainsi que

avec u₂(A) = 0. Ainsi,

Si l'on considère maintenant le segment [AD] :

et ainsi

L'intérêt de faire la moyenne apparaît si l'on fait tourner le losange, il faut alors définir deux angles et .

---

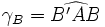
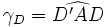
Note : dans l'article Déformation élastique, l'angle γ défini vaut le double de l'angle défini ici.

---

Définition générale

L'opérateur des déformations est un opérateur visant à caractériser en un point la déformation du milieu, c’est-à-dire la variation de longueur d'un segment suite à la transformation subie par le milieu.

On considère le segment AB qui se transforme en A' B'. Cet opérateur permet de quantifer |A' B'|²-|AB|².

On décrit la transformation de chaque point du milieu par une fonction (suffisamment régulière) : telle que

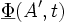
On introduit alors le concept de déformation, pour mesurer la variation de distance entre deux points du solide suite à la transformation .

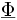
On cherche à avoir une mesure de |A' B'|²-|AB|².

Or on a

On peut donc écrire :

où

est le gradient de la transformation.

On obtient donc :

On pose :

est l'opérateur des déformations de Green-Lagrange

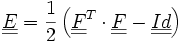
Si on introduit le vecteur déplacement

on obtient :

Si l'on fait l'hypothèse des petites déformations, on obtient l'opérateur des déformations linéarisé :