Cube - Définition

Introduction

Cube
Type	Polyèdre régulier
Faces	Carré
Éléments :  · Faces  · Arêtes  · Sommets  · Caractéristique	6 12 8 2
Faces par sommet	3
Sommets par face	4
Isométries	Oh
Dual	Octaèdre
Propriétés	Deltaèdre régulier et convexe, zonoèdre
modifier

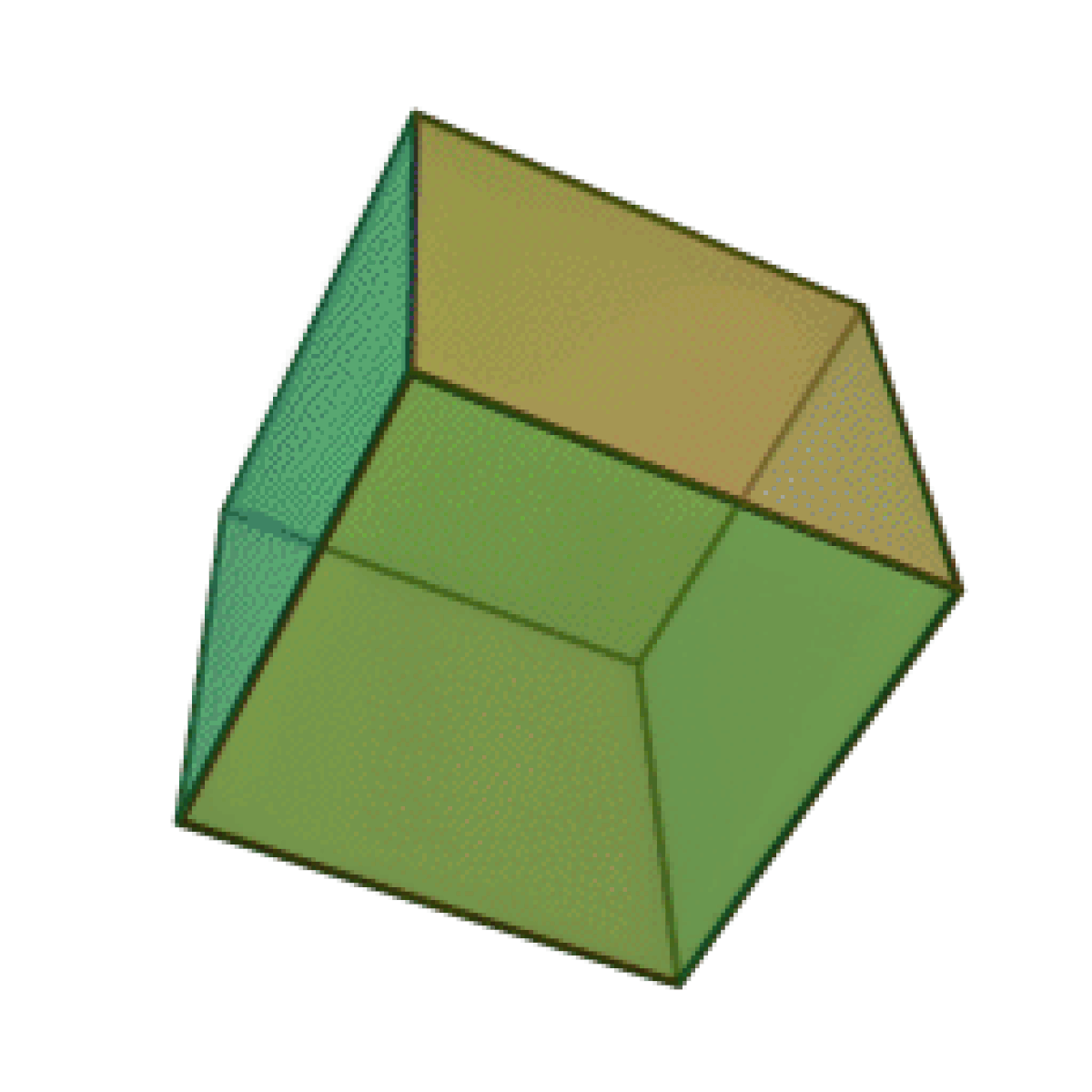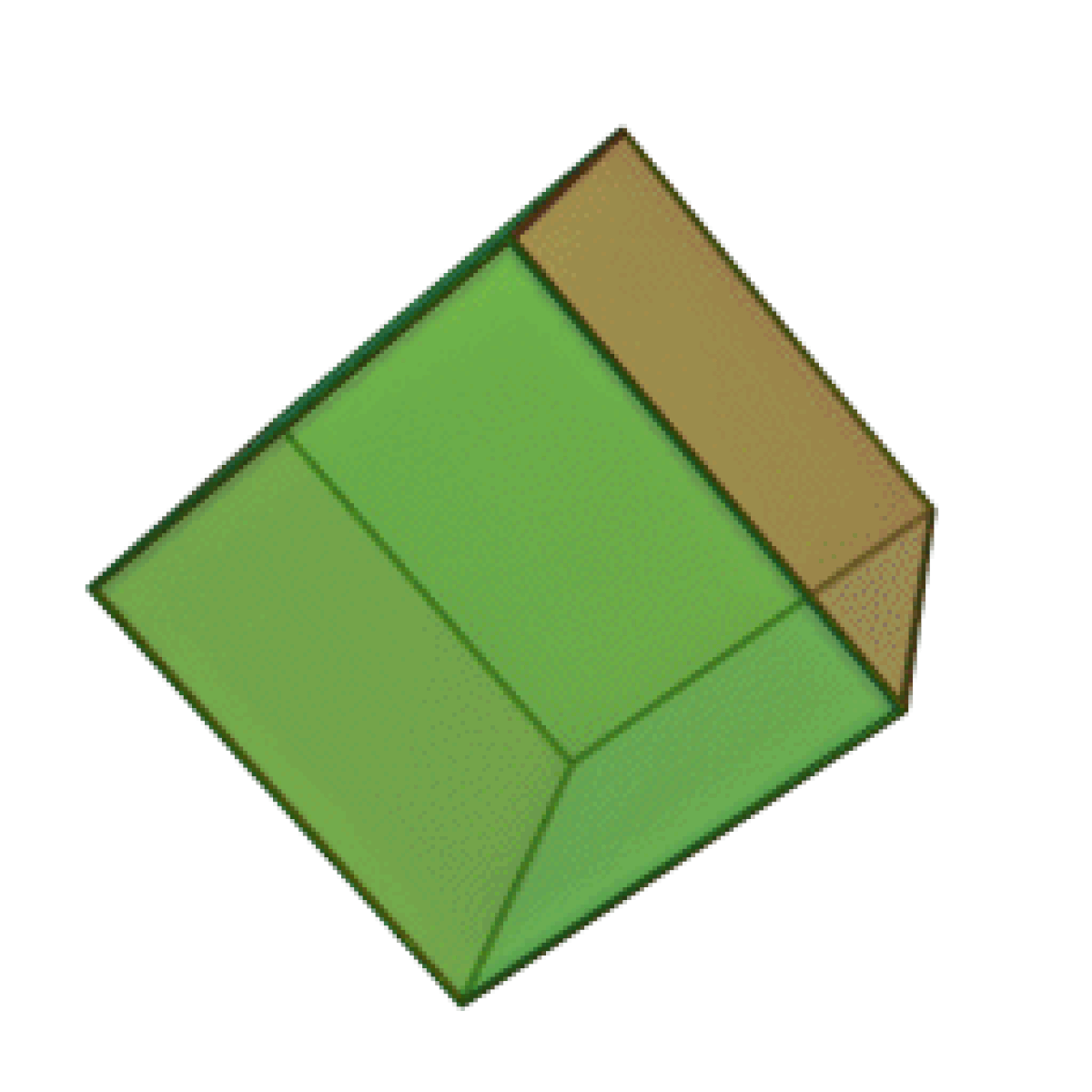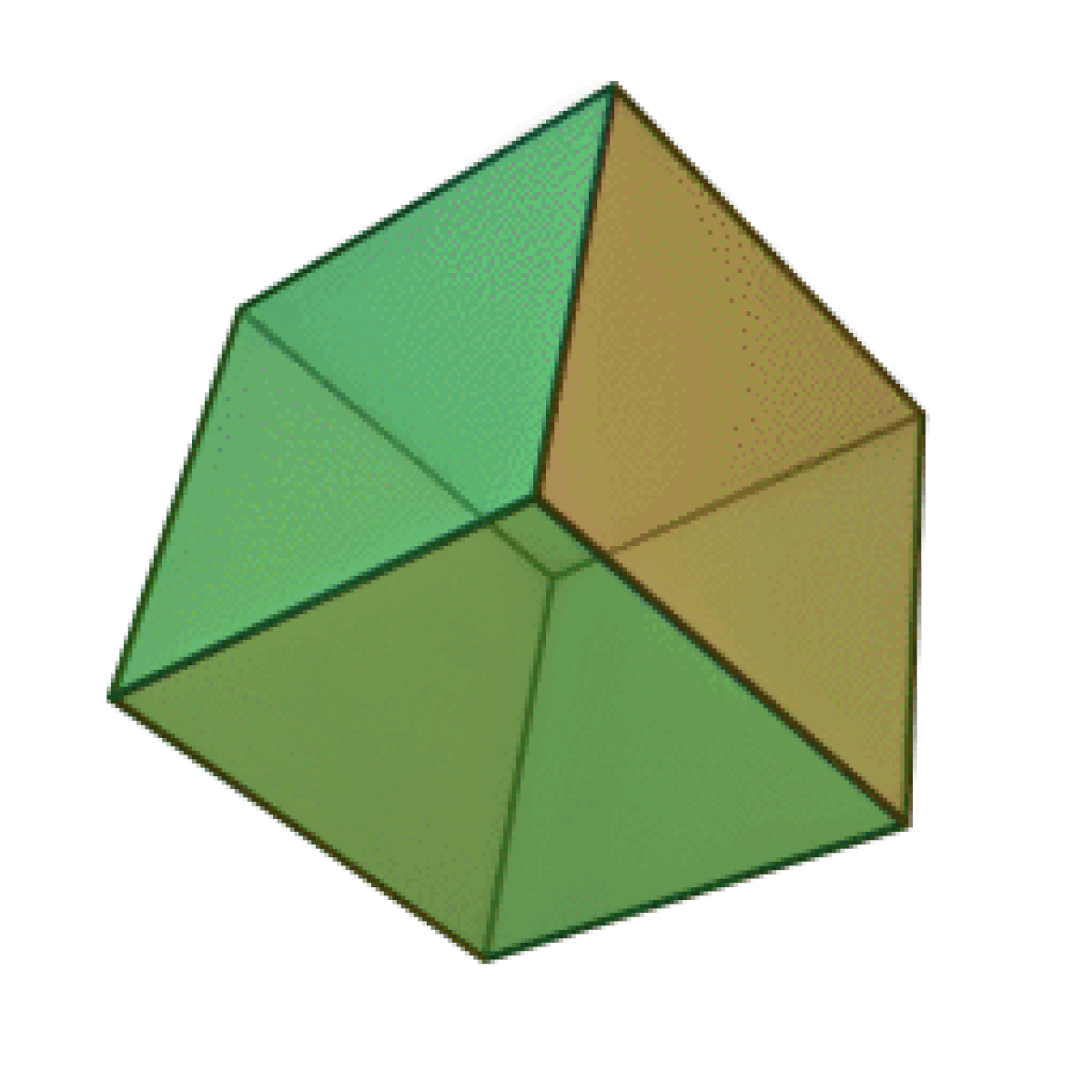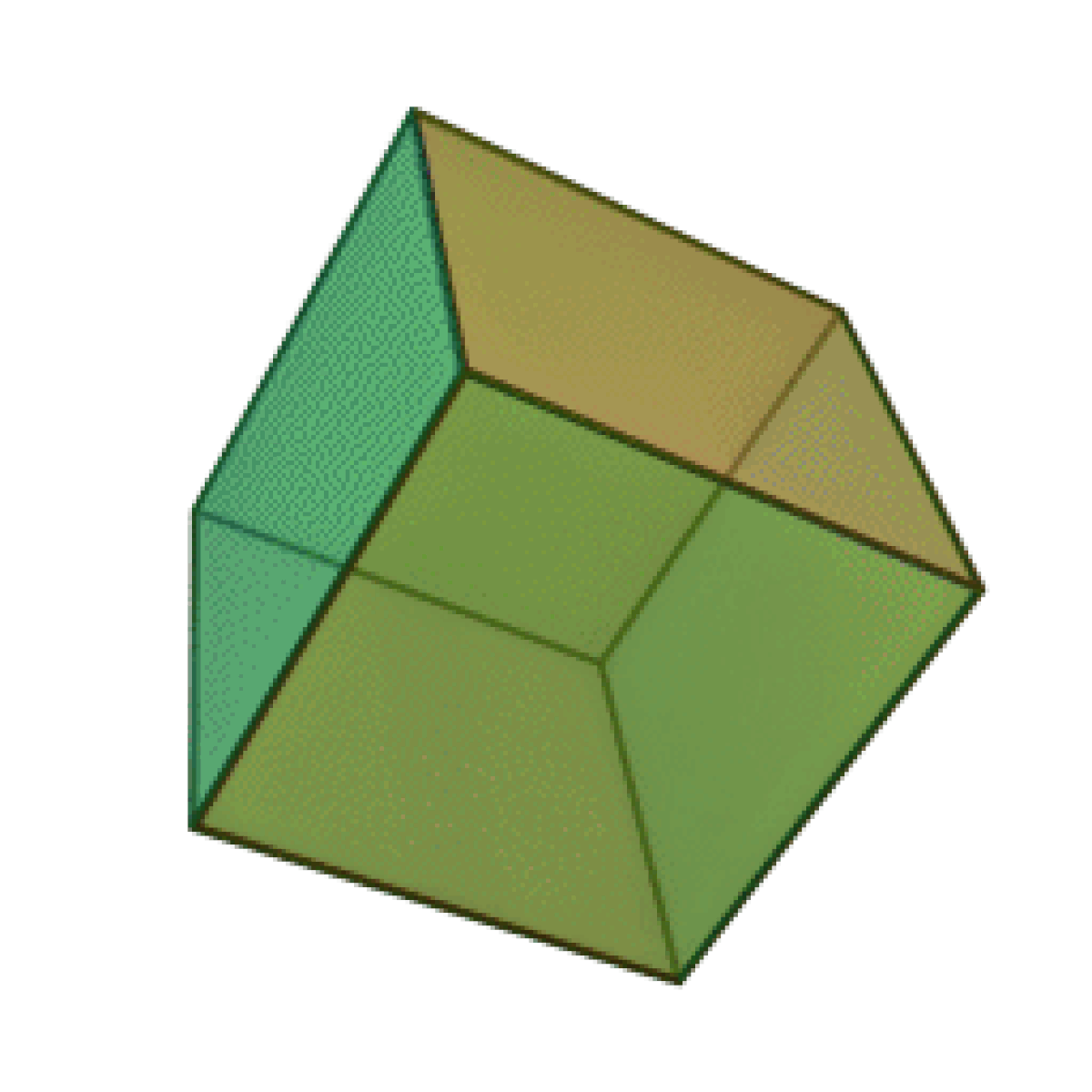
En géométrie euclidienne, un cube est un prisme dont toutes les faces sont carrées. Les cubes figurent parmi les solides les plus remarquables de l'espace. C'est un des cinq solides de Platon, le seul ayant exactement 6 faces, 12 arêtes et 8 sommets. Son autre nom est « hexaèdre régulier ».

L'étymologie du terme cube est grecque ; cube provient de kubos, le dé.

Le terme de cube, appliqué à un nombre, désigne la valeur obtenue en multipliant ce nombre par lui-même et en remultipliant le résultat par le nombre initial. Cette expression s'est imposée durant la période où l'algèbre géométrique était omniprésente, le carré d'un nombre était vu comme la surface d'un carré de côté le nombre initial et le cube d'un nombre comme le volume d'un cube de côté le nombre initial . L'expression « a³ » peut se lire « a au cube » et « a cube ».

Le squelette du cube, l'ensemble de ses sommets reliés par ses arêtes, forme un graphe appelé graphe hexaédrique.

Géométrie

Le cube est un des cinq solides de Platon. Un cube appartient à la famille des prismes droits. Il possède 8 sommets et 12 arêtes. De plus :

• Deux arêtes ayant une extrémité commune sont orthogonales.
• Les faces opposées sont parallèles. Les faces adjacentes sont perpendiculaires
• Tous les angles dièdres sont droits.
• Les diagonales s'intersectent en un unique point, le centre de symétrie du cube, l'isobarycentre des huit sommets.

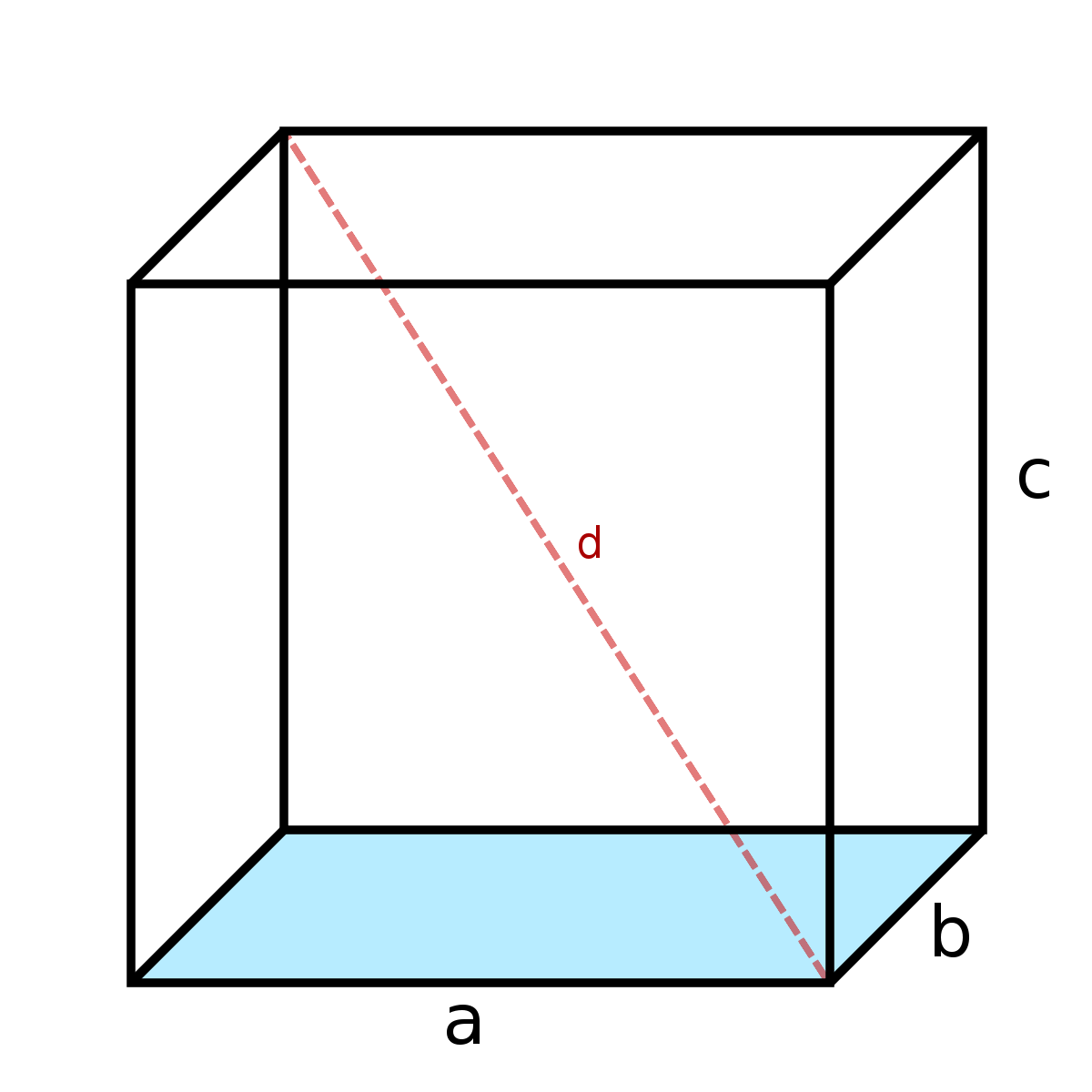
Mais par définition ses arêtes sont toutes de longueur égale, disons a. Ses faces sont donc des carrés, de même superficie, égale à a². De fait :

• son aire vaut donc 6 × a² ;
• son volume vaut a³ ;
• la longueur d'une diagonale vaut  ;
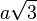
• la sphère circonscrite a donc pour rayon  ;
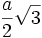
• la sphère tangente aux arêtes a pour rayon  ;
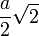
• la sphère inscrite a pour rayon  ;
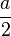
• l'angle entre la diagonale et chacun des plans adjacent vaut .

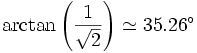
C'est l'expression de son volume qui a conduit à l'utilisation du mot cube en algèbre.

Groupe des isométries

Le cube est l'un des polyèdres offrant le plus de symétries :

• 3 axes de rotation d'ordre 4 : axes passant par le centre de deux faces opposées ;
• 6 axes de rotations d'ordre 2 : axes passant par le milieu de deux arêtes opposées ;
• 4 axes de rotation d'ordre 3 : axes passant par deux sommets opposés ;
• la symétrie de centre O ;
• 9 plans de symétrie : 3 plans médiateurs des arêtes, 6 plans passant par deux arêtes opposées.

Une isométrie du cube est entièrement définie par l'image d'un sommet et des trois arêtes issues de ce sommet (repère de l'espace). Ce sommet peut avoir pour image l'un quelconque des 8 sommets du cube. La première arête a alors 3 images possibles, la seconde arête deux images seulement et l'image de la dernière arête est alors déterminée. Ceci prouve que les isométries laissant le cube globalement invariant sont au nombre de 8 × 3 × 2 = 48. Ces isométries se partagent en 24 isométries positives et 24 isométries négatives. Les isométries positives possèdent toutes le point O comme invariant : on dénombre alors 23 rotations plus l'identité.

On retrouve alors les axes de rotations précédents :

• 3 axes de rotation générant 3 rotations d'angle non nul, soit 9 rotations ;
• 6 axes de rotation générant 1 rotation d'angle plat, soit 6 rotations ;
• 4 axes de rotation générant 2 rotations d'angle non nul, soit 8 rotations.

ainsi que les 9 symétries par rapport à un plan générées par les 9 rotations d'angle plat composées avec la symétrie de centre O.

Ce qui prouve que l'inventaire était bien exhaustif.

Ce groupe est le plus vaste de ceux des polyèdres réguliers qui peuvent paver l'espace. L'analyse associée se trouve dans l'article réseau (géométrie).