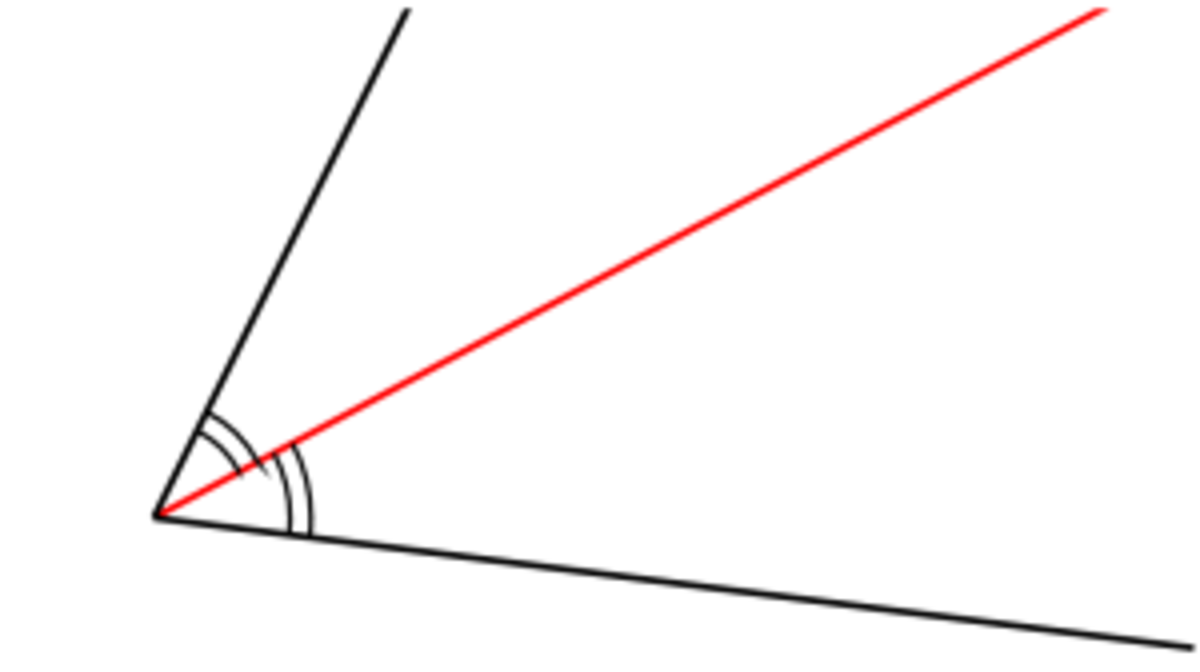
Bissectrice - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, de façon informelle, une bissectrice est une demi-droite qui coupe un angle en deux parties égales. Cette notion peut être généralisée en nommant ainsi la droite qui se superpose à la demi-droite.
Définition
La bissectrice d'un secteur angulaire le partage en deux secteurs angulaires superposables. C'est une demi-droite issue du sommet du secteur angulaire.
Proposition : l'axe de symétrie d'un secteur angulaire porte la bissectrice de ce secteur angulaire.
Si A, B et I sont trois points non alignés, on note B' le symétrique de B par rapport à la droite (AI).
- Comme A est sur l'axe de symétrie, AB = AB'. Le triangle BAB' est donc isocèle de sommet A
- par construction, (AI) est un (l')axe de symétrie du triangle.
- La symétrie axiale préserve les angles : ∠BAI = ∠IAB'. [AI) est donc la bissectrice de l'angle en A
D'un coup de compas, on peut toujours faire apparaître un triangle isocèle dans un secteur angulaire. L'axe de symétrie du triangle isocèle est aussi axe de symétrie pour le secteur angulaire. CQFD
Remarque : Il peut être commode de décider d'appeler bissectrice tout l'axe et pas seulement la demi-droite contenue dans le secteur angulaire.
Construction géométrique
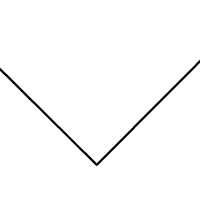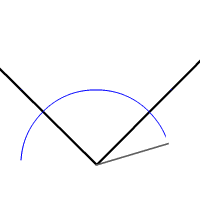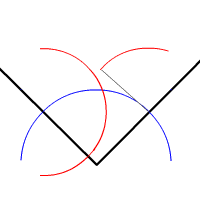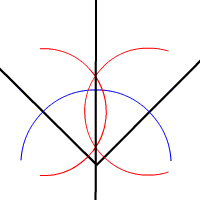
Comme conséquence du théorème de la bissectrice, voici une méthode de construction à la règle et au compas de la bissectrice d'un angle.
- Pointer le compas au sommet de l'angle et tracer un premier arc de cercle. Marquer les points d'intersection de cet arc avec les deux côtés de l'angle.
- Pointer successivement le compas aux points d'intersection tracer deux arcs de cercle de même rayon (en gardant le même écartement du compas entre les deux opérations). Marquer le point d'intersection de ces deux arcs.
- Relier le sommet de l'angle et le point d'intersection des deux derniers cercles et vous avez tracé la bissectrice de l'angle.
Il vous faut un compas, un crayon gris bien taillé, et une feuille.
Théorème de la bissectrice
Théorème de la bissectrice — Tout point de la bissectrice d'un angle est à égale distance des côtés de cet angle.
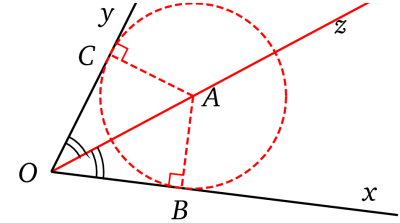
On note
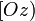
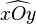
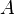
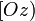
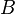
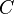
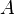
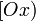
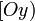
- On sait que la distance de A à
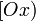
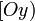
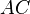
- par hypothèse,
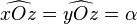
- Les relations trigonométriques dans les triangles rectangles OAC et OAB donnent :
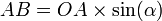
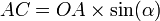
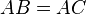
Réciproquement, un point équidistant des côtés de l'angle est sur la bissectrice de cet angle. on peut donc énoncer:
Théorème de la bissectrice (bis) — La bissectrice d'un angle est l'ensemble des points à égale distance des côtés de cet angle.
Corollaire : La bissectrice [Oz) d'un angle xOy est le lieu des centres des cercles tangents aux côtés [Ox) et [Oy) de cet angle.
- Soit M un point de la bissectrice. On construit le point H sur le côté [Ox) tel que la droite (MH) est perpendiculaire à la demi-droite [Ox). On construit de même le point H' sur le côté [Oy). D'après le théorème, MH = MH', donc H et H' sont sur un même cercle C de centre M. De plus [Ox) est perpendiculaire au rayon [MH] donc [Ox) est tangente au cercle C. De même [Oy) est tangente au cercle C.
- Réciproquement, on suppose que C est un cercle de centre M, tangent à [Ox) en un point K et tangent à [Oy) en un point L. Comme (MK) est perpendiculaire à [Ox), MK est la distance de M à [Ox). De même ML est la distance de M à[Oy). Par hypothèse MK=ML donc M est sur la bissectrice de xOy d'après le théorème (bis). CQFD
Applications :
- Construction au compas de la bissectrice
- Les bissectrices d'un triangle se rencontrent au centre du cercle inscrit.