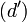Théorème de Pappus - Définition

Source: Wikipédia sous licence CC-BY-SA 3.0.
La liste des auteurs de cet article est disponible ici.

- Introduction - Démonstration à l'aide des applications projectives - Énoncé du théorème - Notions connexes - Démonstration à l'aide du théorème de Ménélaüs - Théorème ou axiome?

Introduction

Le théorème de Pappus est un résultat de géométrie présentant deux particularités :

D'abord, parmi tous les théorèmes de géométrie, c'est celui qui demande les hypothèses minimales. Il porte sur deux triplets de points arbitraires respectivement pris sur deux droites coplanaires quelconques. Il ne demande donc comme connaissance que celle de l'alignement de trois points et ne nécessite par exemple ni métrique, ni orthogonalité… On dit qu'il est un théorème de géométrie projective.

Ensuite, ce théorème est le générateur de tous les théorèmes de géométrie euclidienne par l'enchaînement suivant

D'après un résultat obtenu par D. Hilbert, le théorème de Pappus permet de démontrer le théorème des triangles homologiques.

Dans Leçons de géométrie projective du célèbre géomètre F. Enriqués, on lit : …en se servant du théorème des triangles homologiques […] on pourrait déduire tous les théorèmes de géométrie projective plane. (voir page 46 de son livre)

Enfin la géométrie projective contient la géométrie euclidienne comme cas particulier.

On trouvera tous les détails sur ces développements dans les références données en fin d'article. Cette particularité remarquable explique que certains auteurs aient conféré le statut d'axiome à ce théorème, voir axiomes de plans projectifs.

Démonstration à l'aide des applications projectives

Démonstration du théorème

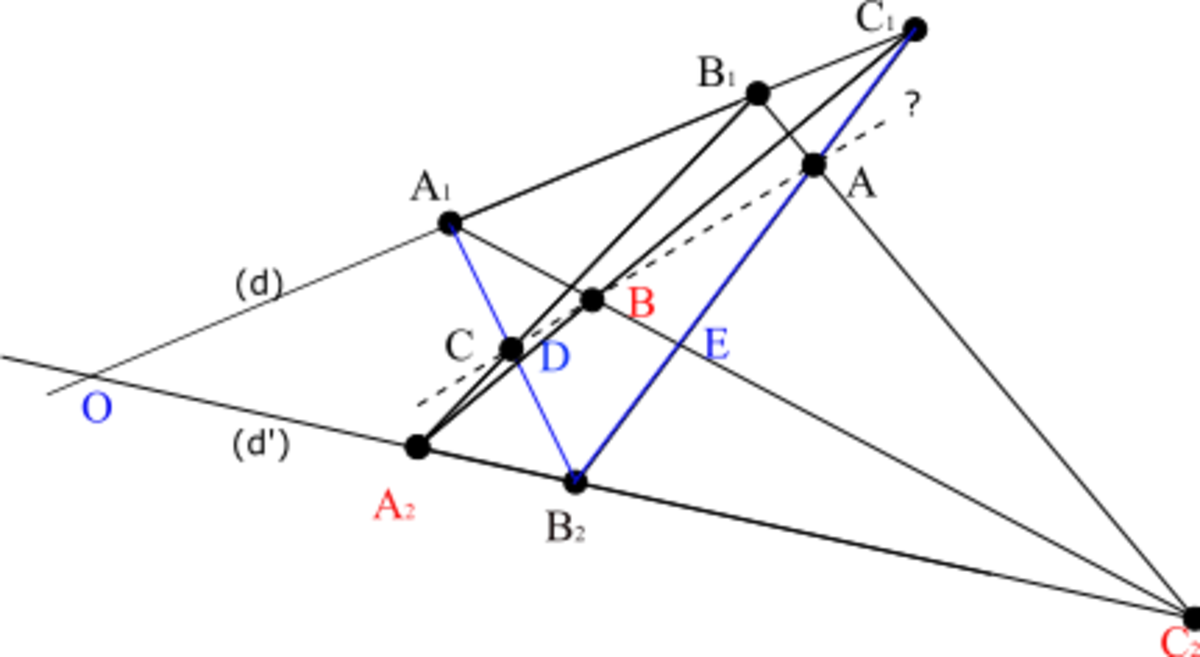
On construit les points O intersection de (d) et (d'), D intersection de $(A 1 B 2)$ et $(A 2 C 1)$ et E intersection de $(A 1 C 2)$ et $(C 1 B 2)$

On considère la projection centrale p de la droite $(A 1 B 2)$ sur la droite (d) de centre $A 2$

$A 1$ a pour image $A 1$
C a pour image $B 1$
D a pour image $C 1$
$B 2$ a pour image O

On considère la projection centrale q de la droite (d) sur la droite $(B 2 C 1)$ de centre $C 2$

$A 1$ a pour image E
$B 1$ a pour image A
$C 1$ pour image $C 1$
O a pour image $B 2$

Par l'application projective q o p de la droite $(A 1 B 2)$ sur la droite $(B 2 C 1)$

$A 1$ a pour image E
C a pour image A
D a pour image $C 1$
$B 2$ a pour image $B 2$

Si on regarde maintenant la projection centrale r de la droite $(A 1 B 2)$ sur la droite $(B 2 C 1)$ de centre B

$A 1$ a pour image E
D a pour image $C 1$
$B 2$ a pour image $B 2$

Or, une application projective d'une droite sur une autre est entièrement déterminée par l'image de trois points distincts. Les transformations q o p et r coïncident sur $A 1$ , D et $B 2$ . Elles sont donc égales et $r (C) = A$ . Les points A, B et C sont donc alignés.

Énoncé du théorème

Théorème de Pappus

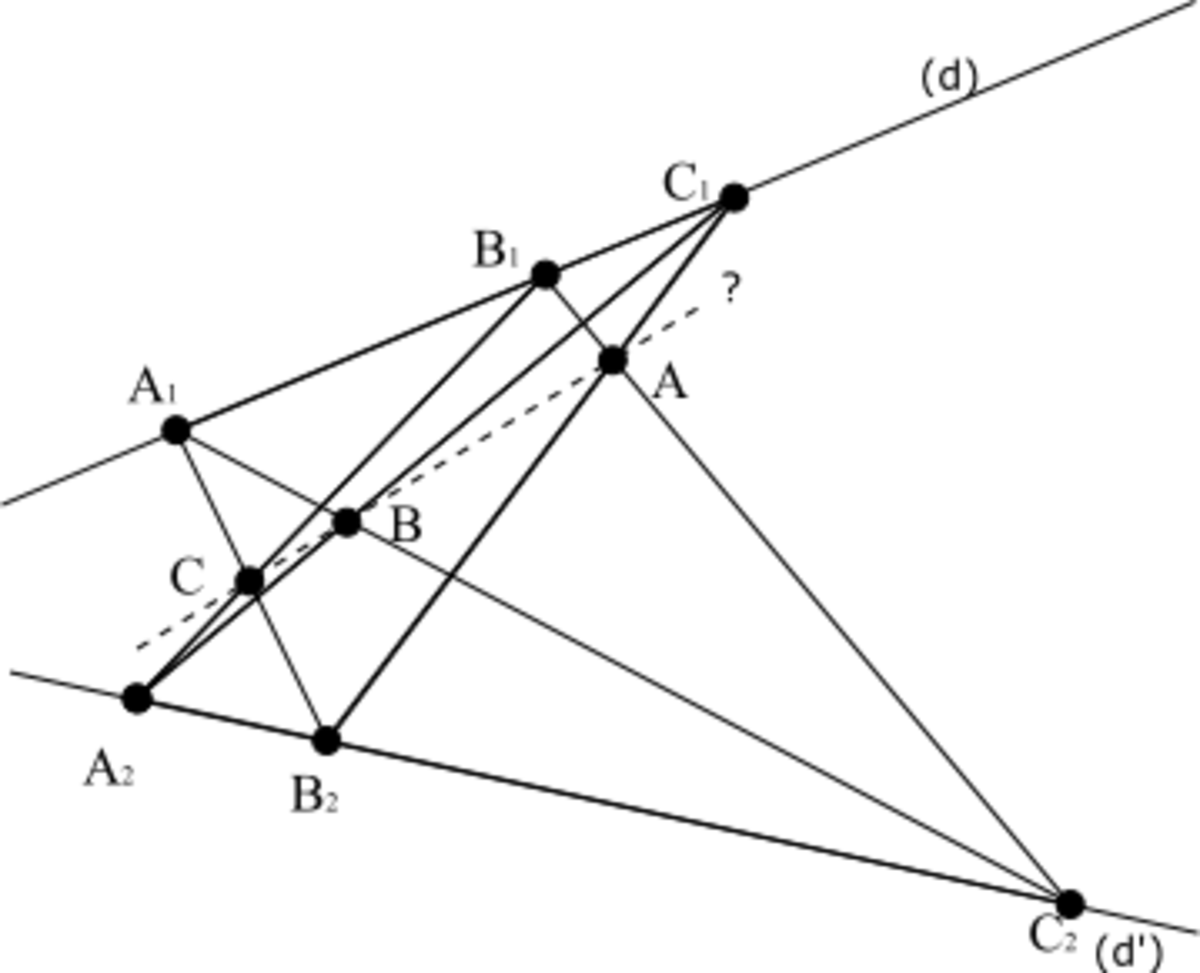
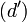
Dans un plan, soient $A 1$ , $B 1$ , $C 1$ trois points distincts alignés sur une droite $(d)$ , et soient $A 2$ , $B 2$ , $C 2$ trois autres points distincts alignés sur une autre droite $(d^\prime)$ alors les points

$A$ intersection de $(B 2 C 1)$ avec $(C 2 B 1)$
$B$ intersection de $(A 2 C 1)$ avec $(C 2 A 1)$
$C$ intersection de $(A 2 B 1)$ avec $(B 2 A 1)$

sont alignés.

Il s'agit d'un théorème de géométrie projective donc les points considérés peuvent être propres ou impropres. Dans le cas où tous les points sont propres, on obtient une configuration du type ci-contre.

Remarques :

si l'on note $(Δ)$ la droite portant les points A,B,C alors les assertions suivantes sont équivalentes (en géométrie projective) :

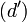
-- les trois droites $(d)$ , $(d^\prime)$ et $(Δ)$ sont concourantes ;

-- les trois droites $(A 1 A 2)$ $(B 1 B 2)$ $(C 1 C 2)$ sont concourantes ;

-- les six droites « croisillons » $(B 2 C 1)$ $(C 2 B 1)$ $(A 2 C 1)$ $(C 2 A 1)$ $(A 2 B 1)$ $(B 2 A 1)$ sont tangentes à une même conique.

-- Les deux droites $(d)$ et $(d^\prime)$ peuvent être considérées comme une conique dégénérée : pour l'hexagramme $A 1 B 2 C 1 A 2 B 1 C 2$ , le théorème de Pappus-Pascal affirme l'alignement des points $A$ , $B$ et $C$ .