Théorie de l'information - Définition
La liste des auteurs de cet article est disponible ici.
Mesure de la quantité d'information
Quantité d'information : cas élémentaire
Considérons N boîtes numérotées de 1 à N. Un individu A a caché au hasard un objet dans une de ces boîtes. Un individu B doit trouver le numéro de la boîte où est caché l'objet. Pour cela, il a le droit de poser des questions à l'individu A auxquelles celui-ci doit répondre sans mentir par OUI ou NON. Mais chaque question posée représente un coût à payer par l'individu B (par exemple un euro). Un individu C sait dans quelle boîte est caché l'objet. Il a la possibilité de vendre cette information à l'individu B. B n'acceptera ce marché que si le prix de C est inférieur ou égal au coût moyen que B devrait dépenser pour trouver la boîte en posant des questions à A. L'information détenue par C a donc un certain prix. Ce prix représente la quantité d'information représentée par la connaissance de la bonne boîte : c'est le nombre moyen de questions à poser pour identifier cette boîte. Nous la noterons I.
EXEMPLE :
Si N = 1, I = 0. Il n'y a qu'une seule boîte. Aucune question n'est nécessaire.
Si N = 2, I = 1. On demande si la bonne boîte est la boîte n°1. La réponse OUI ou NON détermine alors sans ambiguïté quelle est la boîte cherchée.
Si N = 4, I = 2. On demande si la boîte porte le n°1 ou 2. La réponse permet alors d'éliminer deux des boîtes et il suffit d'une dernière question pour trouver quelle est la bonne boîte parmi les deux restantes.
Si N = 2k, I = k. On écrit les numéros des boîtes en base 2. Les numéros ont au plus k chiffres binaires, et pour chacun des rangs de ces chiffres, on demande si la boîte cherchée possède le chiffre 0 ou le chiffre 1. En k questions, on a déterminé tous les chiffres binaires de la bonne boîte. Cela revient également à poser k questions, chaque question ayant pour but de diviser successivement le nombre de boîtes considérées par 2 (méthode de dichotomie).
On est donc amené à poser I = log2(N), mais cette configuration ne se produit que dans le cas de N événements équiprobables.
Quantité d'information relative à un évènement
Supposons maintenant que les boîtes soient colorées, et qu'il y ait n boîtes rouges. Supposons également que C sache que la boîte où est caché l'objet est rouge. Quel est le prix de cette information? Sans cette information, le prix à payer est log(N). Muni de cette information, le prix à payer n'est plus que log(n). Le prix de l'information « la boîte cherchée est rouge » est donc log(N) − log(n) = log(N / n).
On définit ainsi la quantité d'information comme une fonction croissante de
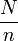
- N le nombre d'évènements possibles
- n le nombre d'éléments du sous-ensemble délimité par l'information
Afin de mesurer cette quantité d'information, on pose :
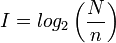
I est exprimé en bit (ou logon, unité introduite par Shannon[citation nécessaire], de laquelle, dans les faits, bit est devenu un synonyme), ou bien en nat si on utilise le logarithme naturel à la place du logarithme de base 2.
Cette définition se justifie, car l'on veut les propriétés suivantes :
- l'information est comprise entre 0 et ∞ ;
- un évènement avec peu de probabilité représente beaucoup d'information (exemple : « Il neige en janvier » contient beaucoup moins d'information que « Il neige en août » pour peu que l'on soit dans l'hémisphère nord) ;
- l'information doit être additive.
Remarque : lorsqu'on dispose de plusieurs informations, la quantité d'information globale n'est pas la somme des quantités d'information. Ceci est dû à la présence du logarithme. Voir aussi : information mutuelle, information commune à deux messages, qui, dans l'idée, explique cette « sous-additivité » de l'information.
Entropie, formule de Shannon
Supposons maintenant que les boîtes soient de diverses couleurs : n1 boîtes de couleur C1, n2 boîtes de couleur C2, ..., nk boîtes de couleurs Ck, avec n1 + n2 + ... + nk = N. La personne C sait de quelle couleur est la boîte recherchée. Quel est le prix de cette information ?
L'information « la boîte est de couleur C1 » vaut log N/n1, et cette éventualité a une probabilité n1/N. L'information « la boîte est de couleur C2 » vaut log N/n2, et cette éventualité a une probabilité n2/N...
Le prix moyen de l'information est donc n1/N log N/n1 + n2/N log N/n2 + ... + nk/N log N/nk. Plus généralement, si on considère k évènements disjoints de probabilités respectives p1, p2, ..., pk avec p1 + p2 + ... + pk = 1, alors la quantité d'information correspondant à cette distribution de probabilité est p1 log 1/p1 + ... + pk log 1/pk. Cette quantité s'appelle entropie de la distribution de probabilité.
L'entropie permet donc de mesurer la quantité d'information moyenne d'un ensemble d'évènements (en particulier de messages) et de mesurer son incertitude. On la note H :
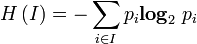
avec
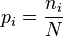
Codage de l'information
On considère une suite de symboles. Chaque symbole peut prendre deux valeurs s1 et s2 avec des probabilités respectivement p1 = 0,8 et p2 = 0,2. La quantité d'information contenue dans un symbole est :
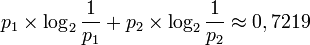
Si chaque symbole est indépendant du suivant, alors un message de N symboles contient en moyenne une quantité d'information égale à 0,72N. Si le symbole s1 est codé 0 et le symbole s2 est codé 1, alors le message a une longueur de N, ce qui est une perte par rapport à la quantité d'information qu'il porte. Les théorèmes de Shannon énoncent qu'il est impossible de trouver un code dont la longueur moyenne soit inférieure à 0,72N, mais qu'il est possible de coder le message de façon à ce que le message codé ait en moyenne une longueur aussi proche que l'on veut de 0,72N lorsque N augmente.
Par exemple, on regroupe les symboles trois par trois et on les code comme suit :
| symboles à coder | probabilité du triplet | codage du triplet | longueur du code |
|---|---|---|---|
| s1s1s1 | 0.8³ = 0.512 | 0 | 1 |
| s1s1s2 | 0.8² × 0.2 = 0.128 | 100 | 3 |
| s1s2s1 | 0.8² × 0.2 = 0.128 | 101 | 3 |
| s2s1s1 | 0.8² × 0.2 = 0.128 | 110 | 3 |
| s1s2s2 | 0.2² × 0.8 = 0.032 | 11100 | 5 |
| s2s1s2 | 0.2² × 0.8 = 0.032 | 11101 | 5 |
| s2s2s1 | 0.2² × 0.8 = 0.032 | 11110 | 5 |
| s2s2s2 | 0.2³ = 0.008 | 11111 | 5 |
Le message s1s1s1s1s1s2s2s2s1 sera codé 010011110.
La longueur moyenne du code d'un message de N symboles est :
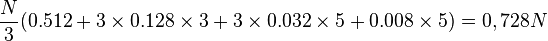
Voir l'article détaillé : théorie des codes.

















































