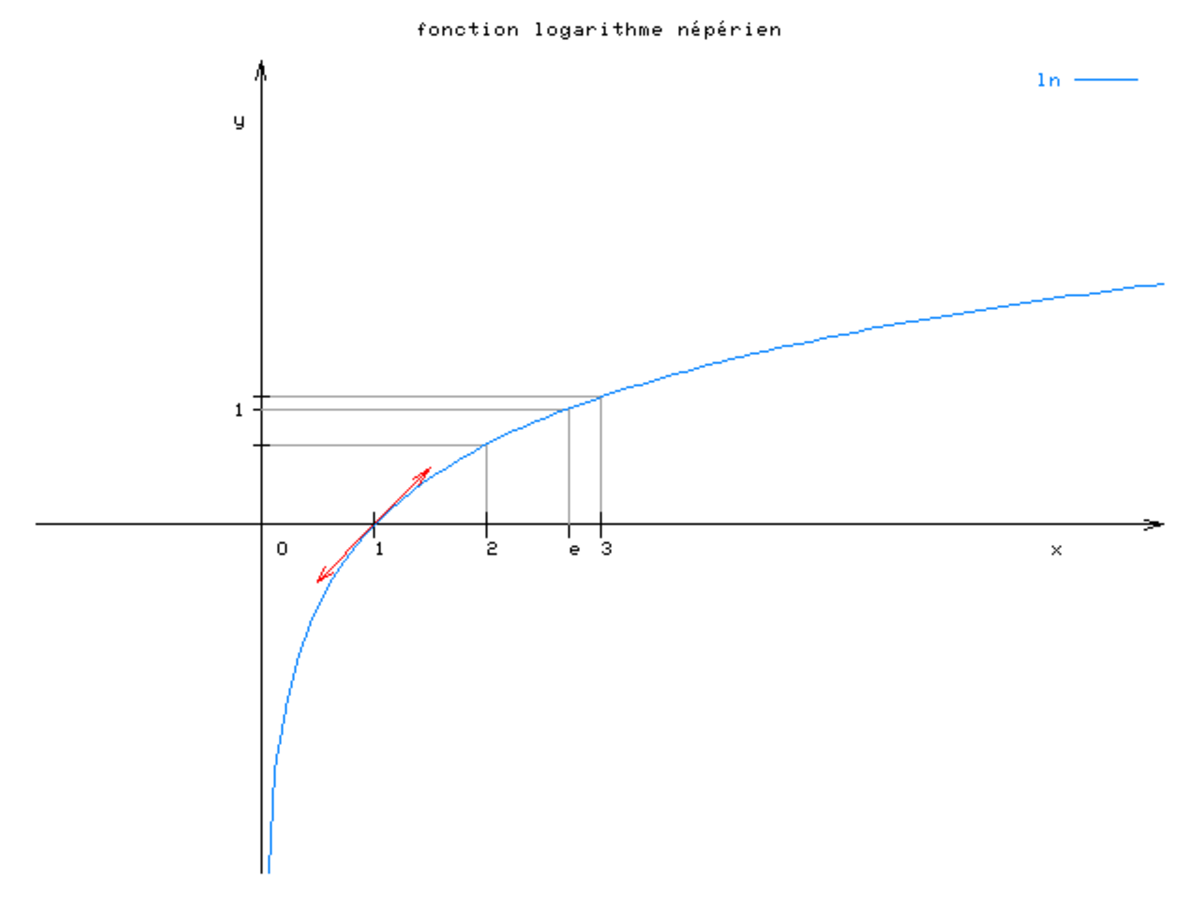
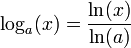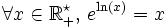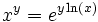Logarithme naturel - Définition
En mathématiques le logarithme naturel ou logarithme népérien, est le logarithme de base e. C'est la réciproque de la fonction exponentielle de base e. C'est la primitive de la fonction inverse définie sur
![]0 ; + \infty[](https://static.techno-science.net/illustration/Definitions/autres/a/abe7a92275e0c5644d5bd5c819fa694e_7de8844c4d1d9aa7fac379e65356ed74.png)
Le logarithme de x est la puissance à laquelle il faut élever e pour trouver x.
Cette fonction a été longtemps notée Log pour la différencier de la fonction log (logarithme décimal). On préfère de nos jours la notation ln.
Fragments d'histoire
Ce logarithme est appelé logarithme népérien en hommage au mathématicien écossais John Napier qui est à l'origine des premières tables logarithmiques. Celles-ci ne furent cependant pas des tables de logarithmes népériens. On date en général la naissance des logarithmes népériens de 1647, date à laquelle Grégoire de Saint-Vincent travaille sur la quadrature de l'hyperbole et démontre que la fonction obtenue vérifie la propriété des fonctions logarithmes (transformation d'un produit en somme). La fonction ln s'est d'ailleurs appelée un certain temps fonction logarithme hyperbolique compte tenu de sa découverte comme aire sous l'hyperbole. Le terme de logarithme naturel apparaît pour la première fois dans une note de Nicolaus Mercator en 1668, quand celui-ci met en place sa série de Mercator. Sa série exploitée par Newton (méthode des fluxions et des suites infinies 1671), permet de calculer assez simplement les valeurs du logarithme de Grégoire de Saint-Vincent. Le calcul des autres logarithmes apparaît alors bien compliqué. Le logarithme de Grégoire de Saint-Vincent devient alors le logarithme le plus "simple" et le plus naturel.
Fonction ln comme primitive de la fonction inverse
Formellement, ln(x) peut être défini comme l'aire du domaine délimité par la courbe représentative de la fonction
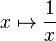
Cette approche, respectueuse de la réalité historique, permet de prouver l'existence de la fonction ln et ses diverses propriétés. La fonction
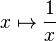
![]0 ; + \infty[](https://static.techno-science.net/illustration/Definitions/autres/a/abe7a92275e0c5644d5bd5c819fa694e_7de8844c4d1d9aa7fac379e65356ed74.png)
Propriétés immédiates
Il est alors immédiat de dire que la fonction ln est définie sur
![]0 ; + \infty[](https://static.techno-science.net/illustration/Definitions/autres/a/abe7a92275e0c5644d5bd5c819fa694e_7de8844c4d1d9aa7fac379e65356ed74.png)
![]0 ; + \infty[](https://static.techno-science.net/illustration/Definitions/autres/a/abe7a92275e0c5644d5bd5c819fa694e_7de8844c4d1d9aa7fac379e65356ed74.png)
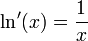
On démontre aisément ses propriétés algébriques en remarquant que la fonction f définie par f(x) = ln(ax) a même dérivée que ln, donc diffère de la fonction ln d'une constante
- f(x) = ln(x) + k
Or f(1) = ln(a) donc k = ln(a) et ln(ax) = ln(a) + ln(x) pour tous réels a et x strictement positifs. La fonction ln est donc bien un cas particulier de fonction logarithme.
C'est la réciproque de la fonction exp - quand celle-ci est définie comme l'unique fonction valant 1 en 0 et égale à sa dérivée. En effet, il suffit de dériver les fonctions
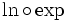
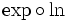

![]0 ; + \infty[](https://static.techno-science.net/illustration/Definitions/autres/a/abe7a92275e0c5644d5bd5c819fa694e_7de8844c4d1d9aa7fac379e65356ed74.png)
Dérivée logarithmique
- Voir article détaillé : dérivation logarithmique
Les propriétés de dérivabilité des fonctions composées permettent de dire que, pour toute fonction réelle dérivable strictement positive, la fonction ln(u) est dérivable de dérivée
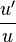
On généralise la propriété à toute fonction dérivable u qui ne s'annule pas : ln( | u | ) est dérivable de dérivée
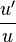
Étude des limites
La fonction logarithme est une fonction tendant vers l'infini en 0 et en
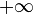
-
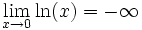
-
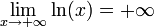
-
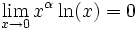
-
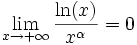
-
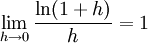
Développement en série
C'est Nicolaus Mercator qui le premier propose le développement en série entière de ln(1 + x) ; le rayon de convergence de ce développement est 1.
Fonction ln comme fonction logarithme
Comme toute fonction logarithme, elle possède les propriétés algébriques suivantes
Le fait que toutes les fonctions logarithmes soient proportionnelles entre elles permet d'obtenir le logarithme de base a en fonction du logarithme népérien:
(pour toutes les propriétés voir : identités logarithmiques)
Fonction ln comme réciproque de la fonction exp
Des égalités
et
-
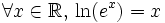
on déduit l'équivalence suivante:
- , pour tout réel x et tour réel y positif.
qui permet de résoudre des équations dans lesquelles l'inconnue apparaît en exposant.
Sa relation avec la fonction exponentielle permet d'exprimer toutes les autres fonctions exponentielles de base a (a réel positif) par
-
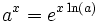
Plus généralement , elle permet de définir xy pour tout réel x strictement positif et tout réel y comme
Cette définition coïncide évidemment avec celle de xr pour r rationnel.
Fonction ln comme fonction de la variable complexe
- Voir article détaillé : logarithme complexe
La question de savoir s'il est possible de prolonger la fonction ln (c'est-à-dire de la définir sur un ensemble plus grand que
![]0 ; + \infty[\;](https://static.techno-science.net/illustration/Definitions/autres/0/0d2969c19864581352c59628e54f9f1d_4343bc0ccad1b6226cb6b414368a0b81.png)
-
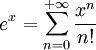
à
-
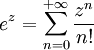
s'est fait de manière naturelle et l'on se serait attendu à ce qu'un passage analogue se fasse pour la fonction ln. Mais il n'existe aucune fonction univoque continue sur
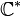
![]0 , + \infty[](https://static.techno-science.net/illustration/Definitions/autres/e/eb8a0ceeec2805d7e3ba7c0591eafa52_68fa31b6b628907eade001f071ed7130.png)
L'existence de plusieurs valeurs possibles pour ln(-1), par exemple, a donné lieu à des échanges de lettres passionnés entre Leibniz et Bernoulli. Le voile sera levé par Euler.
On peut cependant définir le logarithme d'un nombre négatif de la manière suivante
- ln( − a) = ln(a) + iπ pour a réel strictement positif
en référence au fait que
- ln( − a) = ln(eiπa)
et par transfert de propriété
- ln( − a) = ln(a) + iπ
Mais la fonction ainsi définie n'a pas les propriétés algébriques de la fonction logarithme népérien réelle. On peut la rencontrer lorsqu'on travaille avec une calculatrice traitant les nombres complexes : si l'on étudie la fonction
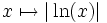
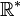
-
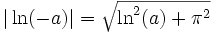
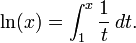
![\ln(ab) = \ln(a) + \ln(b) \quad \forall (a;b)\in\, ]0 : + \infty[^2](https://static.techno-science.net/illustration/Definitions/autres/8/8d368040dfd783cb1fefd9c7024d9e6d_540b2f2148bc0a96baaa804b091c32cc.png)
![\ln\left(\frac ab\right) = \ln(a) - \ln(b) \quad \forall (a;b)\in\, ]0 : + \infty[^2](https://static.techno-science.net/illustration/Definitions/autres/d/d91473ac07dda8f581720854ea220f0d_2b210c3b973ce9c145dab61826386eff.png)
![\ln(a^n) = n \ln(a) \quad \forall a \in\, ]0 ; + \infty[, \forall n \in \mathbb Z](https://static.techno-science.net/illustration/Definitions/autres/a/aa08335497383b527fe5072274c9ad3b_d70177c1d564165ce5acd11213f5bb6f.png)
![\ln(a^r) = r \ln(a) \quad \forall a \in\, ]0 ; + \infty[, \forall r \in \mathbb Q](https://static.techno-science.net/illustration/Definitions/autres/b/b603d2842043acf02ba341e04a16c624_27e9d2c2d16ff32e3f02736fcc70b9a4.png)