Théorie des langages - Définition

Introduction

La théorie des langages a pour objectif de comprendre le fonctionnement des langages, vus comme moyen de communication, d'un point de vue mathématique.

Un langage est un ensemble de mots. Un mot (ou lexème) est une combinaison de signes élémentaires. L'ensemble de ces signes élémentaires est appelé alphabet. La fonction associant l'alphabet au langage est appelée grammaire. On peut associer à une grammaire un automate permettant de déterminer si un mot fait partie d'un langage.

Parmi les applications pratiques de la théorie des langages, on trouve en particulier les compilateurs, en informatique

Mots

On se donne un ensemble X, appelé alphabet dont les éléments sont appelés des lettres.

• Un mot de longueur k est un k-uplet de lettres u = (a₁,a₂,...,a_k).
• est l'ensemble des mots de longueur k
• est l'ensemble des mots.
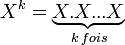
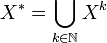
• ε ou () est le mot vide de longueur 0.
• On définit sur , une loi de composition interne appelée concaténation.

(de longueur n + m).

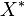
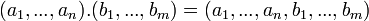
Cette loi de composition interne est associative et admet le mot vide pour élément neutre, par conséquent est un monoïde, appelé monoïde libre sur .

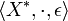
Remarque: Tout mot (a₁,...,a_n) est égal au concaténé (a₁).(a₂)...(a_n). En identifiant les mots de longueur 1 aux lettres, on écrit donc le mot sous la forme:

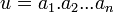
Langages

Un ensemble de mots sur X est appelé un langage. Les langages peuvent être caractérisés par les moyens qui permettent de les décrire, par exemple :

• les langages rationnels peuvent être décrits par des automates finis ou des expressions rationnelles ;
• les langages algébriques peuvent être décrits par des grammaires hors-contexte ou des automates à piles ;
• ...