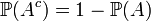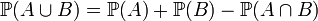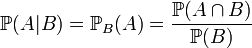Théorie des probabilités - Définition
La liste des auteurs de cet article est disponible ici.
La théorie des probabilités aujourd'hui
Certaines distributions peuvent être un mélange de distributions discrètes et continues, et donc n'avoir ni densité de probabilité ni fonction de masse. La distribution de Cantor constitue un tel exemple. L'approche moderne des probabilités résout ces problèmes par l'utilisation de la théorie de la mesure pour définir un espace probabilisé et aboutir aux axiomes des probabilités développés par Kolmogorov
Un espace probabilisé comporte trois parties:
- un univers Ω: L'univers est l'ensemble de tous les résultats possibles de l'évenement aléatoire. Par exemple pour un dé a 6 faces l'univers est Ω ≡ {1, 2, 3, 4, 5, 6}.
- un ensemble d'événements
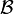
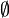
- {ø, {1}, {2}, {3}, {4}, {1,2}, {1,3}, {1,4}, {2,3}, {2,4}, {3,4}, {1,2,3}, {1,2,4}, {1,3,4}, {2,3,4}, {1,2,3,4}}. On remarque que cette tribu contient l'ensemble vide ø et Ω={1,2,3,4}. Ceci est le cas pour toutes les tribus.
- une mesure
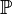
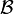
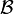
Dans cette optique, pour des événements deux à deux disjoints (c'est-à-dire, d'intersection deux à deux vide) A1, A2, A3…, la probabilité de leur union apparaît comme la somme de leurs probabilités, ou, avec les notations mathématiques,
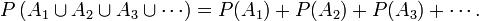
C'est le troisième et dernier axiome des probabilités. Par exemple, et toujours pour un dé à 6 faces, la probabilité de tirer un 1 ou un 2
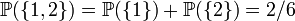
En plus de permettre une meilleure compréhension et une unification des théories discrètes et continues des probabilités, l'approche de la théorie de la mesure nous permet aussi de parler de probabilités en dehors de

Principes fondamentaux
La probabilité d'un événement donné A,
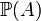
| Évènement | Probabilité |
|---|---|
| probabilité de A |
|
| probabilité de ne pas avoir A |
|
| probabilité d'avoir A ou B |
|
| probabilité conditionnelle de A, sachant B |
|
| probabilité d'avoir A et B |
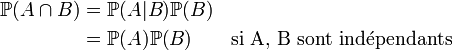
|
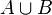
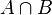
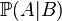
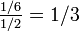
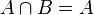
![\mathbb{P}(A)\in[0,1]\,](https://static.techno-science.net/illustration/Definitions/autres/e/e80064214aea988389b07fc8d173b9cd_028c7bf986e62f211a6400ff85dfd11e.png)