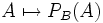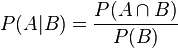Probabilité conditionnelle - Définition

La notion de probabilité conditionnelle permet de tenir compte dans une prévision d'une information complémentaire. Par exemple, si je tire au hasard une carte d'un jeu, j'estime naturellement à une chance sur quatre la probabilité d'obtenir un cœur ; mais si j'aperçois un reflet rouge sur la table, je corrige mon estimation à une chance sur deux. Cette seconde estimation correspond à la probabilité d'obtenir un cœur sachant que la carte est rouge. Elle est conditionnée par la couleur de la carte ; donc, conditionnelle.

La pratique n'est cependant pas toujours aisée, comme le montrent certains paradoxes tels que le paradoxe des deux enfants, le paradoxe des deux enveloppes, le paradoxe des trois pièces de monnaie et le paradoxe des prisonniers. D'où la nécessité d'une définition rigoureuse.

Définition

En théorie des probabilités, la probabilité conditionnelle d'un évènement A, sachant qu'un autre évènement B de probabilité non nulle s'est réalisé (ou probabilité de A, sachant B) est le nombre noté P(A/B) défini par :

Le réel P(A | B) se lit " probabilité de A, sachant B ".

P(A | B) se note aussi P_B(A).

Mathématiquement, soient , un espace probabilisé et B un évènement de la tribu de probabilité non nulle (non quasi-impossible). À tout évènement A de , nous associons le nombre noté P(A | B) ou P_B(A) défini par:

.

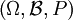
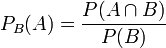
Nous pourrions vérifier que l'application P_B définie par est une probabilité.