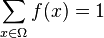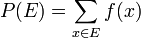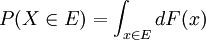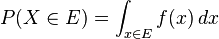Théorie des probabilités - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
La théorie des probabilités est l'étude mathématique des phénomènes caractérisés par le hasard et l'incertitude. Les objets centraux de la théorie des probabilités sont les variables aléatoires, les processus stochastiques, et les événements: ils traduisent de manière abstraite des événements non déterministes ou des quantités mesurées qui peuvent parfois évoluer dans le temps d'une manière apparemment aléatoire. En tant que fondement mathématique des statistiques, la théorie des probabilités est essentielle à la plupart des activités humaines qui nécessitent une analyse quantitative d'un grand nombre de mesures. Les méthodes de la théorie des probabilités s'appliquent également à la description de systèmes complexes dont on ne connait qu'en partie l'état, comme en mécanique statistique. Une grande découverte de la physique du vingtième siècle fut la nature probabiliste de phénomènes physiques à une échelle microscopique, décrite par la mécanique quantique.
Historique
La théorie mathématique des probabilités trouve ses origines dans l'analyse de jeux de hasard par Gerolamo Cardano au seizième siècle, et par Pierre de Fermat et Blaise Pascal au dix-septième siècle. Bien qu'un simple pile ou face ou un lancer de dés soit un événement aléatoire, en les répétant de nombreuses fois on obtient une série de résultats qui va posséder certaines propriétés statistiques, que l'on peut étudier et prévoir. Deux résultats mathématiques fondamentaux à ce propos sont la loi des grands nombres et le théorème de la limite centrale.
Initialement, la théorie des probabilités considérait surtout les événements discrets, et ses méthodes étaient principalement combinatoires. Mais des considérations analytiques ont forcé l'introduction de variables aléatoires continues dans la théorie. Cette idée prend tout son essor dans la théorie moderne des probabilités, dont les fondations ont été posées par Andreï Nikolaevich Kolmogorov. Kolmogorov combina la notion d'univers, introduite par Richard von Mises et la théorie de la mesure pour présenter son système d'axiomes pour la théorie des probabilités en 1933. Très vite, son approche devint la base incontestée des probabilités modernes.
Théorie des probabilités discrète
La théorie discrète des probabilités s'occupe d'événements dans le cadre d'un univers fini ou dénombrable.
Exemples: lancer de dés, expériences avec des paquets de cartes, et marche aléatoire.
Définition classique: Initialement, la probabilité d'un événement était définie comme le nombre de cas favorables pour l'événement, divisé par le nombre total d'issues possibles à l'expérience aléatoire.
Par exemple, si l'événement est obtenir un nombre pair en lançant le dé, sa probabilité est donnée par
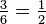
Définition moderne : La définition moderne commence par un ensemble appelé univers, qui correspond à l'ensemble des issues possibles à l'expérience dans la définition classique. Il est noté
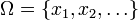
On définit ensuite un événement comme un ensemble d'issues, c'est-à-dire un sous-ensemble de Ω. La probabilité d'un évènement E est alors définie de manière naturelle par :
Ainsi, la probabilité de l'univers est 1, et la probabilité de l'événement impossible (l'ensemble vide) est 0.
Pour revenir à l'exemple du lancer de dés, on peut modéliser cette expérience en se donnant un univers Ω = {1;2;3;4;5;6} correspondant aux valeurs possibles du dé, et une fonction f qui à chaque
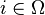
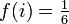
Théorie des probabilités continue
La théorie des probabilités continue s'occupe des événements qui se produisent dans un univers continu (par exemple la droite réelle).
Définition classique: La définition classique est mise en échec lorsqu'elle est confrontée au cas continu (cf. paradoxe de Bertrand).
Définition moderne Si l'univers est la droite réelle


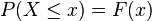
La fonction de répartition doit satisfaire les propriétés suivantes :
-

-
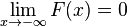
-
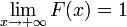
Si

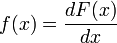
Pour un ensemble

Si la densité de probabilité existe, on peut alors la réécrire :
Tandis que la densité de probabilité n'existe que pour les variables aléatoires continues, la fonction de répartition existe pour toute variable aléatoire (y compris les variables discrètes) à valeurs dans

Ces concepts peuvent être généralisés dans les cas multidimensionnel sur

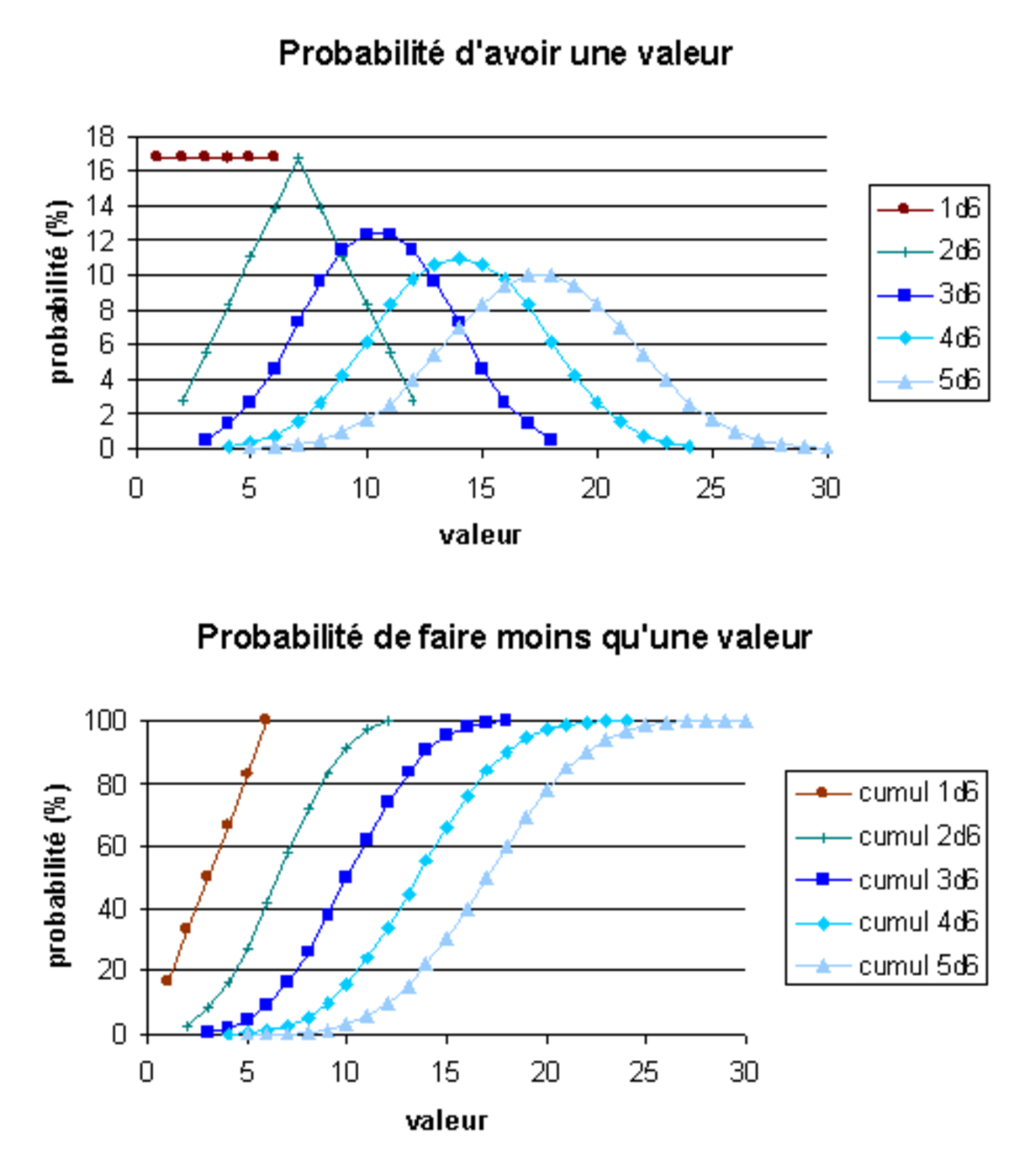
![f(x)\in[0,1]\mbox{ pour tout }x\in \Omega](https://static.techno-science.net/illustration/Definitions/autres/0/0e77ec055bf042c11b977174cb518c4d_b55a81070377755958271de08c9cada0.png)