Triangle de Kobon - Définition

Introduction

Le problème des triangles de Kobon est un problème de géométrie combinatoire non-résolu qui fut énoncé pour la première fois par le mathématicien Kobon Fujimura. Le problème pose la question suivante : quel est le nombre maximal de triangles distincts pouvant être construits à l'aide d'un nombre donné de segments de droite ?

Le problème fut popularisé par Martin Gardner en 1983.

Borne supérieure

Saburo Tamura a montré que, pour n segments de droite, le nombre maximal de triangles qu'il est possible de construire, noté N(n), est inférieur ou égal à ( désigne la fonction partie entière).

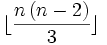
En 2007, Johannes Bader et Gilles Clément ont affiné cette borne : N(n) est inférieur ou égal à où χ est la fonction caractéristique, égale ici à 1 si n est congru à 0 ou 2 modulo 6 et 0 dans les autres cas. La limite donnée par Tamura ne peut donc pas être atteinte lorsque cette fonction caractéristique n'est pas nulle.

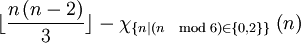
Solutions connues

Des solutions maximales, égales à la borne supérieure, sont connues pour 3, 4, 5, 6, 7, 8, 9, 13, 15 et 17 droites. Dans les autres cas, le nombre maximal de triangles n'est pas connu, même si connait des configurations qui se rapproche de cette borne supérieure. Pour 10 et 11 droites, la meilleure solution connue n'est que d'un triangle de moins que la borne donnée par Tamura. Pour 12, 16 et 18 droites, deux triangles de mois.

Le tableau suivant résume, pour les premières valeurs du nombre de segments, la valeur de la borne supérieure ainsi que celle de la meilleure solution connue (indiquée en gras lorsqu'il s'agit d'une solution réellement maximale).

Dans l'encyclopédie électronique des suites entières, la suite est classée sous le numéro A006066.