Valeur moyenne (quantique) - Définition

Exemple dans l'espace de configuration

Par exemple, considérons une particule quantique dans un espace à 1 dimension, dans la représentation de l'espace de configuration. Ici, l'espace de Hilbert est , l'espace des fonctions de carré sommable sur l'axe réel. Les vecteurs sont représentés par des fonctions , que l'on appelle « fonctions d'onde ». Le produit scalaire est donné par . Les fonctions d'onde ont une interprétation directe en termes de distributions de probabilité :

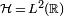
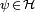
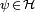
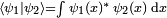
donne la probabilité de trouver la particule dans un intervalle infinitésimal de longueur autour du point .

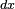
Considérons comme observable l'opérateur de position , qui agit sur les fonctions d'onde par

.

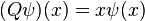
L'espérance quantique, ou valeur moyenne, de sur un grand nombre de systèmes indépendants identiques est donnée par

.

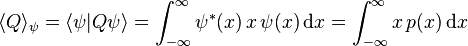
On notera que la valeur moyenne ne converge que si l'intégrale converge, ce qui n'est pas le cas pour tous les vecteurs . Ceci est dû au fait que l'opérateur de position est non borné, et il faut choisir dans son domaine de définition.

En général, la valeur moyenne de toute observable peut être calculée en remplaçant par l'opérateur convenable. Par exemple, pour calculer le moment moyen, on utilise la représentation de l'opérateur moment dans l'espace de configuration, . Explicitement, cette valeur moyenne est donc

.

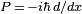
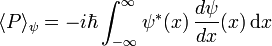
Tous les opérateurs ne possèdent pas en général une valeur moyenne. Un opérateur qui a une valeur moyenne réelle est appelé une observable, et sa valeur peut être directement mesurée expérimentalement.