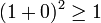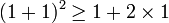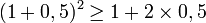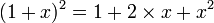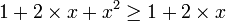Variable (mathématiques) - Définition

Variables mathématiques et variables informatiques

En mathématiques comme en informatique les variables symbolisent des objets et peuvent prendre des valeurs qui sont des éléments d'un certain ensemble.

Mais dans certains langages de programmation, les variables représentent des données qui varient au cours du temps et peuvent même prendre une valeur fonction de la valeur qu'elles avaient juste avant. Ces variables doivent impérativement prendre une valeur initiale avant l'exécution des instructions et leur contenu peut changer. Elles ont une conception totalement différentes des variables mathématiques.

Par contre dans les langages fonctionnels, les variables se rapprochent un peu plus des variables mathématiques. Mais par exemple, dans certains cas, il n'est pas toujours nécessaire d'indiquer le type des données qu'elles représentent, ce qui reviendrait en mathématiques à ne pas préciser l'ensemble auquel les variables que l'on considère appartiennent.

Variable libre et variable liée

En mathématiques une variable est dite :

• libre si elle est remplaçable par le nom d'un objet appartenant à un ensemble donné ; ainsi dans la formule ouverte « 4x² + x - 3 = 0 », la lettre « x » est une variable libre ; si x est remplacée par une constante a, l'expression « 4a² + a - 3 = 0 » est un énoncé clos ou proposition.
• liée ou muette lorsqu'elle entre dans le champ d'un opérateur, en sorte que son rôle est seulement descriptif. Ainsi en est-il de x, k, i, et t respectivement dans les propositions suivantes :

.

On dit que les opérateurs, respectivement ∀, ∑, ∏ et ∫, lient ces variables : ce sont des signes mutificateurs.

Les variables liées par un quantificateur universel ∀ traduisent l'universalité d'une propriété, c'est-à-dire le fait que la dite propriété est satisfaite par tous les objets d'un certain domaine.

Par exemple, nous remarquons que

Alors nous pouvons conjecturer que:

pour tout nombre x,

Si par un raisonnement cette affirmation est démontrée alors il sera possible de l'utiliser pour n'importe quel nombre donné. Pour démontrer ce théorème, il suffit de considérer une variable x représentant un nombre réel quelconque et de développer:

D'autre part nous savons que tout nombre réel élevé au carré est positif, donc . De plus en ajoutant de chaque côté de cette dernière inégalité , il vient

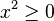
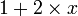
donc

.

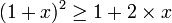
La propriété est donc universelle.

Les variables liées par un quantificateur existentiel ∃ traduisent l'existence d'objets vérifiant une certaine propriété.

Par exemple, le théorème suivant :

deux droites non parallèles du plan se coupent en un point,

affirme qu'il existe un point appartenant à deux droites non parallèles, sans le donner par une formule.

Dans le cadre d'une démonstration, en partant de deux droites non parallèles on pourra utiliser le théorème et affirmer qu'il existe un point M commun à ces deux droites. En fait M est une variable représentant ce point et cette définition de la variable M, va nous permettre de travailler avec ce point.

Voyons encore un autre exemple. Admettons le théorème:

tout nombre (réel) positif peut s'écrire comme un carré.

Considérons 2, on sait que 2 est positif, d'après le théorème il existe un nombre x tel que 2 = x². Encore une fois x est une variable représentant un tel nombre (en fait il y en a deux). Maintenant, on peut utiliser x sans le connaître et calculer par exemple x⁴ − x².

x⁴ − x² = (x²)² − 2 = 2² − 2 = 2.