🔎 Variété algébrique non-singulière - Définition et Explications

- Introduction - Définition - Bibliographie - Propriétés

Introduction

Une variété algébrique non-singulière (ou lisse) est une variété dépourvue de point singulier. C'est le cadre naturel de nombre de théorèmes fondamentaux en géométrie algébrique.

Définition

On dit qu'une variété algébrique $X$ est régulière lorsque son anneau local $O X, x$ est un anneau local régulier pour tout point $x\in X$ .

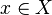
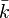
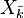
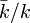
Soit $X$ une variété algébrique sur un corps $k$ . Soit $\bar{k}$ une clôture algébrique de $k$ . On dit que $X$ est non-singulière ou lisse si la variété $X_{\bar{k}}$ obtenue après le changement de base $\bar{k}/k$ est une variété régulière.

Exemples

Les espaces affines $\mathrm{Spm } k[T_1,\ldots, T_n]$ et les espaces projectifs $\mathrm{Proj }k[T_0, \ldots, T_n]$ sont non-singulières.

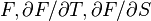
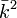
Une courbe plane $Spm(k [T, S] / (F (T, S)))$ est non-singulière si et seulement si les polynômes $F, \partial F/\partial T, \partial F/\partial S$ n'ont pas de zéro commun dans $\bar{k}^2$ (ce qui équivaut à dire qu'ils engendrent l'idéal unité de $k [T, S]$ ).

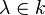
Si $k$ est un corps imparfait (i.e. un corps qui n'est pas parfait), alors il existe $\lambda\in k$ qui ne soit une puissance $p$ -ième, où $p$ est la caractéristique de $k$ . Soit $k' = k [T] / (T p - λ)$ l'extension radicielle définie par la racine $p$ -ième de $λ$ . Alors $Spm(k')$ est une variété algébrique sur $k$ , régulière mais pas non-singulière.

Remarque Être régulière est une propriété absolue de la variété algébrique, alors qu'être non-singulière dépend du corps de base que l'on considère. Dans l'exemple ci-dessus, $Spm(k')$ n'est pas non-singulière en tant que $k$ -variété, mais elle l'est en tant que $k'$ -variété.

Bibliographie

Propriétés

Si $X$ est non-singulière, alors elle est régulière. L'inverse est vrai si $k$ est parfait.

Critère jacobian: Soit $X = Spm[T 1,..., T n] / (F 1,..., F m)$ une variété algébrique affine connex de dimension $d$ . Alors $X$ est non-singulière si et seulement si le rang de la matrice jacobienne $J a c x (F 1,..., F m)$ est égal à $n - d$ pour tout $x$ .

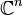
Soit $X$ une variété algébrique complexe (i.e. définie sur le corps des nombres complexes). Soit $X an$ l'espace analytique complexe associé à $X$ . Alors $X$ est non-singulière si et seulement si $X an$ est une variété analytique complexe, c'est-à-dire localement biholomorphe à un ouvert d'un ${\mathbb C}^n$ .

Si $X$ est non-singulière et connexe de dimension n, alors $X$ est irréductible et même intègre, et le faisceau des formes différentielles sur $X$ est localement libre de rang n. Autrement dit, c'est un fibré vectoriel de rang n (appelé le fibré cotangent) sur $X$ .

Structure locale: Contrairement aux variétés analytiques complexes ou différentielles, une variété algébrique, même non-singulière, n'est pas localement (pour la topologie de Zariski) isomorphe à un ouvert d'un espace affine. Mais cela devient vrai si l'on remplace la topologie de Zariski par la topologie étale. En termes plus concrets, tout point d'une variété algébrique non-singulière possède un voisinage ouvert (de Zariski!) qui est un revêtement étale d'un espace affine. En géométrie algébrique, un rêvetement étale est un morphisme plat et non-ramifié.