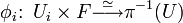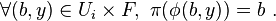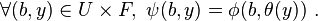Fibré - Définition

Introduction

En mathématiques, un espace fibré est la donnée d'un espace topologique appelé espace total muni d'une projection continue sur un autre espace appelé base, telle que la préimage de chaque point soit homéomorphe à un espace fixe appelé fibre. Cette projection est a priori supposée localement triviale, c'est-à-dire que tout point de la base admet un voisinage dont la préimage s'identifie à un produit cartésien de ce voisinage et de la fibre, par le biais d'homéomorphismes appelés trivialisations ou cartes. Le groupe de structure est alors un groupe d'homéomorphismes de la fibre permettant le passage d'une trivialisation à l'autre.

Cette définition généralise donc la projection d'un produit cartésien sur l'un de ses facteurs.

Définition formelle

Un espace fibré localement trivial peut se présenter comme la donnée d'une application continue π (projection ou pied) entre deux espaces topologiques séparés E et B (espace total et base), d'un espace séparé F (fibre) sur lequel agit un groupe G (groupe de structure) et d'un ensemble d'homéomorphismes (cartes)

où la famille (U_i) décrit un recouvrement ouvert de B, satisfaisant les conditions suivantes :

1. Les cartes commutent avec les projections :

   

2. Les changements de carte sont induits par des sections dans le groupe de structure, autrement dit pour tout couple de cartes (φ, ψ) définies sur un même ouvert U×F il existe une application continue θ de U dans G telle que :

   

L'ensemble des cartes est en général supposé maximal satisfaisant ces conditions, c'est-à-dire que tout homéomorphisme commutant avec les projections et compatible avec les autres cartes est aussi une carte.

Un espace fibré est dit trivialisable s'il admet une carte ayant l'espace total pour image. Il est dit trivial lorsqu'une telle carte est précisée, ce qui l'identifie comme espace fibré au produit cartésien de la base et de la fibre.

Une réduction du groupe de structure est la donnée d'un sous-ensemble de cartes dont la réunion des images est l'espace total et qui reste maximal pour un groupe de structure plus petit. Une trivialisation est donc une réduction du groupe de structure au groupe trivial.

Un fibré de fibre F et de base B se dit parfois « en F sur B ».

Types de fibrés

• Un revêtement est un espace fibré dont la fibre est discrète.
• Un fibré vectoriel est un espace fibré dont la fibre est un espace vectoriel euclidien et le groupe de structure est le groupe linéaire. C'est le cas des fibrés tangent et cotangent sur une variété différentielle.
• Un fibré différentiel est un fibré pour lequel l'espace total, la base et la fibre sont des variétés différentielles

.

• Un fibré principal est un fibré pour lequel le groupe de structure agit librement et transitivement sur la fibre, autrement dit si la fibre peut s'identifier au groupe de structure muni de l'action à droite.

Exemples et contre-exemples

• Le ruban de Möbius muni de la projection sur un cercle médiateur est un espace fibré non trivial, de fibre un intervalle réel et dont le groupe de structure peut se réduire à deux éléments (l'identité et une réflexion).
• La bouteille de Klein est un fibré en cercles sur le cercle dont le groupe de structure se réduit aussi à deux éléments.
• La fibration de Hopf est un fibré en cercles sur la sphère, dont le groupe de structure se réduit au groupe des isométries positives du cercle.
• La projection du premier quadrant sur sa bissectrice est une fibration qui ne définit pas un fibré, car la préimage de l'origine est réduite à un point tandis que la préimage de tout autre point de la bissectrice est un segment d'intérieur non vide.