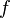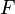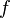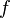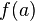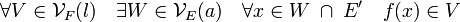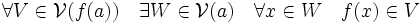Voisinage (mathématiques) - Définition

Limite et continuité en un point

Le formalisme des voisinages permet d'exprimer simplement les notions de limite et de continuité en un point.

Limite

Soit un espace topologique et un sous espace de . Soit une fonction de dans un espace topologique. Soit un point de l'adhérence de , la fonction admet comme limite au point si et seulement si l'image réciproque d'un voisinage de est un voisinage de dans . L'expression de la limite, notée , prend alors la forme suivante :

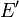
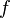
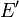
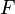
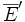
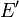
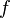
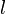
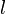
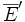
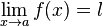
Continuité

Soit une fonction d'un espace topologique dans et soit un point élément du domaine de définition de . La fonction est continue au point si et seulement si l'image réciproque d'un voisinage de est un voisinage de . L'expression de la continuité au point prend alors la forme suivante :