Voisinage (mathématiques) - Définition
La liste des auteurs de cet article est disponible ici.
Introduction
En mathématiques, la notion de voisinage correspond à une approche axiomatique équivalente à celle de la topologie. La topologie traite plus naturellement les notions globales comme la continuité, qui s'entend ici comme la continuité en tout point. En revanche, pour les propriétés locales comme la continuité en un point ou la limite, le formalisme des voisinages est souvent plus simple.
Voisinage dans un espace topologique
Dans un espace topologique, un voisinage d'un point est un sous-ensemble contenant un ouvert contenant ce point. Soit



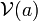

-
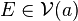
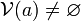
-
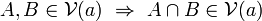
-
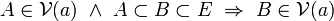
-
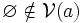
Nous venons de démontrer que les voisinages de


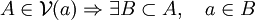
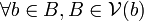
(on retrouve donc que
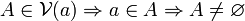
Base de voisinages
L'ensemble des voisinages d'un point est vaste. L'analyse des filtres pour l'inclusion nous indique qu'il nous suffit de connaître une base de filtre pour définir cet ensemble de voisinages. La définition, déduite directement du concept de base de filtre, est donc la suivante : Une base de voisinages d'un point


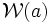


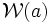
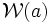
Un voisinage de

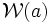
Topologie définie à partir des voisinages
La section précédente montre que les axiomes de la topologie définissent les voisinages en chaque point. On peut alors définir axiomatiquement l'ensemble des voisinages. Cette définition nous permet de définir une topologie.
Soit


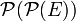
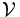
- est un filtre sur

-
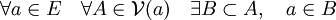
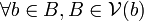
Considérons alors l'ensemble des parties de

Exemples
Le cas des entiers positifs
Il est possible de compléter
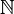
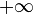
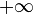
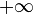
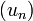


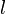
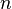
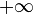
Le cas des nombres réels
Dans l'ensemble des réels, on définit les voisinages d'un réel a de la manière suivante:
-
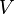

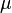
![]a - \mu; a + \mu[\, \subset V](https://static.techno-science.net/illustration/Definitions/autres/1/1c1bc01ff67043326a47d099878e6cf8_fa5268e941b9d16eb83a21c8b3f36f5f.png)

Exprimons alors les notions de limite et de continuité pour une fonction
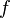

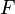
Soit


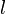
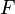
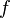
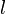

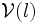
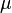
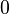
![]a - \mu; a + \mu[\,](https://static.techno-science.net/illustration/Definitions/autres/6/6f0f2909cae079c0b23373c90c4598de_7a6e9ef6239cd94676c5e6f0f0cc3dd0.png)

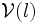
La continuité en


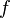
Dans le cas des fonctions réelles de la variable réelle, on obtient:
Pour la continuité on a:
Extension de la droite réelle
Il est possible d'étendre la droite réelle avec les valeurs


- Voisinage de


![]M; + \infty[\, \subset V](https://static.techno-science.net/illustration/Definitions/autres/a/a0edf05bf6e93d5eb1f9a0e5bcb4cefd_0762af2515279c68ebdc19b3851d572f.png)
- Voisinage de


![]-\infty; M [\, \subset V](https://static.techno-science.net/illustration/Definitions/autres/b/bf9349a025d0e3ac045a20ee88df188d_8cc350ba2d7d8ee90eb15b944a07db6e.png)
Remarque: On peut remarquer que la droite réelle étendue avec les voisinages précédents forme bien une topologie. En revanche cette topologie n'est pas déduite de la distance usuelle. En effet, les points limites de la droite réelle n'ont pas de distance vis à vis des autres points.
Dans le cas des fonctions réelles de la variable réelle, on obtient:
Espace métrique
Tout espace métrique est muni d'une topologie déduite. En effet, soit






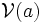
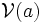
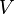
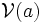


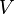
-
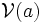
- Tout élément
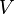
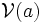


- Enfin soit
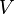
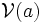



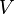
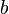
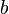
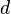

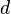

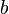
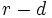


Nous venons de démontrer que les axiomes des ensembles de voisinages sont bien satisfaits, ce qui montre que l'application de

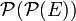
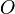

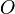

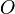
Exprimons alors les notions de limite et de continuité pour une fonction
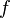

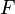
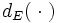
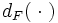

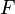
Soit


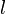
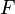
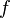
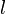


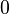
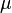
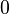

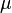

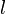

La continuité en


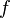
L'ensemble
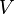
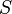
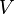
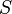
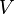
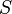


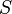


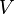
Exemple : dans l'ensemble des réels muni de la distance issue de la valeur absolue, l'ensemble
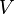
est un voisinage de l'ensemble

Topologie faible
Il existe des topologies qui ne sont pas associées à des espaces métriques. La topologie faible en est un exemple.

![\forall V \in \mathcal V(l) \quad \exist \mu > 0\quad \forall x \in ]a - \mu; a + \mu[\;\cap\; E \quad f(x)\in V\quad \Leftrightarrow \quad \lim_{x \to a}f(x)=l\;](https://upload.wikimedia.org/math/4/f/4/4f4a69364a3f2a73d9c2d965b715e78b.png)
![\forall V \in \mathcal V(f(a)) \quad \exist \epsilon > 0\quad \forall x \in ]a - \mu; a + \mu[\;\cap\; E \quad f(x)\in V\;](https://upload.wikimedia.org/math/e/a/d/ead78a8d2e00436457e3ef66c6375b9a.png)