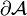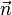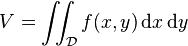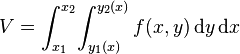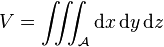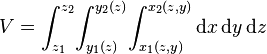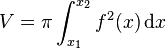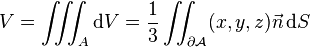Volume - Définition
La liste des auteurs de cet article est disponible ici.
Unités de volume
L'unité de volume du système international est le mètre cube (m³) et ses dérivés (dm³, cm³, mm³). Mais d'autres unités de volume persistent surtout dans les pays anglo-saxons (voir Conversion des unités).
Les volumes de matière liquide ont souvent leurs unités propres (litre, pinte, baril). La mise en place du système métrique a grandement simplifié le nombre d'unités de volume utilisées qui dans l'Ancien Régime en comptait plus de vingt (voir Unités de mesure de l'Ancien Régime).
Pour les gaz où l'on veut connaître la quantité de matière (nombre de molécules) contenue dans un volume donné quelles que soient la pression et la température, deux définitions de correction existent :
- le mètre cube dit normal exprimé en m3(n) correspondant à un volume de gaz ramené sous une pression de 1 013,25 hPa (pression d'une atmosphère normale ou 1 atm) et une température de 0 °C.
- le mètre cube dit standard exprimé en m3(s) correspondant à un volume de gaz ramené sous une pression de 1 013,25 hPa (pression d'une atmosphère normale ou 1 atm) et une température de 25 °C.
Les volumes décrit ci-dessus correspondent à des volumes dit corrigés. Le volume qui ne tient pas compte de ces corrections est dit brut. On rencontre ces volumes dans l'élaboration des débits (voir débit) et du pouvoir calorifique des gaz.
Dans l'Union européenne, de nombreux volumes (et masses), sur les produits de consommation, sont indiqués en quantité estimée. Ils sont marqués comme tel, d'un « e » minuscule.
En mathématiques, l'unité de volume n'apparaît pas dans les formules. Elle est implicitement donnée par le volume du cube unité. Si, par exemple, pour des questions d'échelle, le cube unité a pour arête 2 cm, un volume de X (cube unité) correspond à 8X cm³.
Volume et calcul intégral
Si
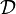
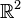
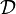
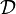
Dans le cas où le domaine
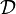
Si

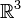


Dans le cas où le domaine

Par linéarité de l'intégration, un domaine difficile à définir peut être partitionné en plusieurs sous-domaines exprimables eux en conditions simples.
Si le domaine

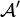
-
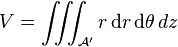
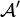
![\R_+\times [0,2\pi] \times \R](https://static.techno-science.net/illustration/Definitions/autres/a/a10c705146178ebf4bbf66a59361c340_a6d30e6f1382187d4c1f800cb8093381.png)
Si le domaine

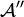
-
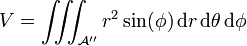
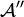
![\R_+\times [0,2\pi]\times [0,\pi]](https://static.techno-science.net/illustration/Definitions/autres/3/3b2f887c8de576ebec1126d3c8d0576e_bcbb2fb92926783353b969a0eb672a14.png)
Dans le cas où le domaine

Enfin, le théorème de flux-divergence permet de réduire le calcul de volume à une intégrale de surface
où