Cube de Hilbert - Définition
En topologie, on appelle cube de Hilbert l'espace produit
![K = \left[0,1\right]^{\mathbb N}](https://static.techno-science.net/illustration/Definitions/autres/2/2018949361ab4610d25ec3e9d9c7f7fc_b0c8859a13c3ebbef8b75374813e9379.png)
Il est homéomorphe à
![\left[0,1\right] \times \left[0,\frac12\right] \times \left[0,\frac13\right] \times \cdots](https://static.techno-science.net/illustration/Definitions/autres/5/5c1978a7f54c943be56379ebc5c5e39f_276ad5d715838e4f3dc8318c3c000b46.png)
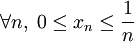
-
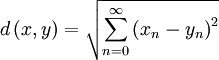
Il s'agit donc d'un espace métrisable.
Il est à base dénombrable (en fait, pour un espace compact, être métrisable ou être à base dénombrable sont des propriétés équivalentes), et possède la propriété universelle suivante :
- " Tout espace métrisable à base dénombrable est homéomorphe à un sous-espace de K. "
Cela fournit en particulier un moyen commode pour compactifier les espaces métrisables à base dénombrable, et aussi un critère pour les classifier selon leur complexité ; par exemple un espace est polonais si et seulement si il est homéomorphe à l'intersection d'une suite d'ouverts de K. On en déduit aussi que tout espace mesurable dénombrablement engendré et séparé est isomorphe à une partie de K munie de la tribu induite par la tribu borélienne de K.

















































