Tribu borélienne - Définition
La tribu borélienne sur un (ou d'un) espace topologique T est la plus petite σ-algèbre sur T contenant tous les ensembles ouverts. Les éléments de la tribu borélienne sont appelés des boréliens.
La tribu de Borel peut, de manière équivalente, se définir comme la plus petite σ-algèbre qui contient tous les sous-ensembles fermés de T. Un sous-ensemble de T est un borélien s’il peut être obtenu à partir d'ensembles ouverts en effectuant une suite dénombrable d'opérations d'unions, d'intersections et de passage au complémentaire, mais, contrairement à l'intuition première, on n'obtient pas ainsi, loin de là, tous les boréliens (quoiqu'on obtienne tous les boréliens usuels) ; en effet la classe obtenue selon ce schéma de construction n'est pas stable pour les réunions et intersections dénombrables, et il faut, pour obtenir tous les boréliens, itérer transfiniment ce schéma - pour plus de détails, voir Classe de Baire.
Un exemple particulièrement important est la tribu borélienne de l'ensemble des nombres réels. Elle intervient dans la mesure de Borel ou de Lebesgue et aussi dans toute probabilité. La tribu des boréliens sur l'ensemble des nombres réels est la plus petite σ-algèbre sur

![\left]a, +\infty\right[](https://static.techno-science.net/illustration/Definitions/autres/5/5a56d24421f819afbc858ff7f7718594_352a06f0fdc009b01224d06e643fbb16.png)
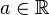


Plus généralement, si la topologie de T est engendrée par une famille dénombrable A, stable par intersection finie, la tribu borélienne associée à T est aussi engendrée par A.
Un espace mesurable est dit lusinien ou standard s'il est isomorphe à une partie borélienne d'un espace polonais muni de la tribu induite par la tribu borélienne. Un théorème de Kuratowski assure que
-
- Tous les espaces mesurables standard non dénombrables sont isomorphes.
Ainsi, du point de vue de la structure borélienne, tous les espaces non-dénombrables usuels sont indistinguables : R est isomorphe à tous les Rn, à l'espace NN, au cube de Hilbert, à l'espace de Cantor, à l'espace de Banach séparable C([0,1]) (ensemble des fonctions continues sur [0,1] muni de la topologie de la convergence uniforme), etc. quoique ces espaces soient très différents du point de vue topologique ou algébrique.

















































