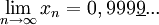Décimale récurrente - Définition

Les décimales récurrentes sont une manière de représenter les décimales de certaines fractions irréductibles qui ne sont pas de la forme k/(2ⁿ5^m). Ces représentations décimales incluent un motif répété de façon infinie à la fin de la fraction (ce motif répété peut être aussi court qu'un simple chiffre).

Pour indiquer la partie de la séquence qui s'étend à l'infini, ou les chiffres répétés peuvent être soulignés, des points peuvent être placés au-dessus des décimales répétées. Lorsque cela est impossible, l'extension peut être représentée par ceci (...), néanmoins, cette manière exprime de façon incertaine quels chiffres doivent être répétés :

• 1/9 = 0,111111111111...
• 1/7 = 0,142857142857...
• 1/3 = 0,333333333333...
• 2/3 = 0,666666666666...
• 7/12 = 0,58333333333...

Calcul de la fraction

Soit une décimale répétée, il est possible de calculer la fraction qui l'a produite. Par exemple :

x = 0,333333...
10x = 3,33333...  (multiplication des deux côtés de la ligne par 10)
9x = 3           (soustraction de la 2ème ligne moins la 1ère)
x = 3/9 = 1/3   (simplification)

Un autre exemple :

x = 0,18181818...
100x = 18,181818...
99x = 18
x = 18/99 = 2*9/11*9 = 2/11 * 9/9 = 2/11 * 1 = 2/11

Après ces exemples, nous pouvons voir que la période des décimales répétées de la fraction n/d sera (au plus) le plus petit nombre k tel que 10^k − 1 est divisible par d.

Par exemple, la fraction 2/7 possède d = 7, et le plus petit k qui donne 10^k − 1 divisible par 7 est k = 6, parce que 999999 = 7 × 142857. La période de la fraction 2/7 est par conséquent 6.

Pourquoi les nombres rationnels doivent avoir leurs décimales terminales répétées

Dans l'idée de convertir un nombre rationnel représenté sous forme de fraction en forme décimale, on peut utiliser une longue division. Par exemple, considérons le nombre rationnel 5/74 :

0,0675
74 \ 5,000000
4 44
560
518
420
370
500

etc. Observons qu'à chaque étape, nous avons un reste ; les restes successifs affichés ci-dessus sont 56, 42 et 50. Lorsque nous arrivons au reste 50 et qu'on abaisse le " 0 ", nous nous retrouvons à diviser 500 par 74. C'est le même problème par lequel nous avions commencé. Par conséquent, les décimales se répètent : 0,0675675675... Nous pouvons revoir des restes déjà vus plus tôt. Les seuls restes possibles — dans ce cas il y en a 74 — sont : 0, 1, 2, ... et 73. Dès que l'on retombe sur un reste déjà obtenu, la séquence entière se répète.

Le cas de 0,99999...

La méthode de calcul des fractions à partir des décimales répétées, spécialement dans le cas de 1 = 0,99999... qui est quelques fois contestée de façon naïve. Un bon argument est que si deux nombres réels sont distincts, alors il existe une infinité d'autres nombres réels entre les deux (strictement). Or, il n'existe aucun autre réel entre 0,99999 (une infinité de 9) et 1. C'est donc un seul et même réel, écrit de deux manières différentes.

On présente parfois aussi la démonstration suivante :

x = 0,99999...
10.x = 9,9999...
10x - x = 9,9999... - 0,99999...
9.x = 9
x = 1

Certains argumentent que, dans la seconde étape ci-dessus, 10.x vaut 9,9999...0 et non 0,999. Mais ce n'est pas le cas ; le RHS ne se termine pas (il est récurrent) et donc il n'y a pas de fin pour laquelle un zéro peut être trouvé.

Pour une preuve moins persuasive mais d'un aspect plus formel, on peut considérer la suite  :

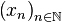
Ce qui donne

, et

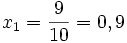
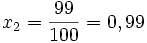
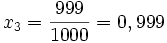
On "voit" alors que

Mais aussi

Ainsi, par unicité des limites.

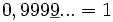
L'exposé ci-dessus utilisant des notations mathématiques plus formelles est d'un aspect plus impressionnant que la preuve arithmétique mais elle est moins persuasive. L'étape cruciale, la division par 10ⁿ n'est pas accomplie actuellement. Mais, la preuve utilisant les limites qui a clairement complété la preuve arithmétique est adéquate et plus simple. Elle peut être suivie même par ceux qui ne comprennent pas les limites.

Généralisant ceci, n'importe quel nombre avec une expression décimale finie (une fraction décimale) peut être écrite d'une seconde manière comme les décimales récurrentes.

Par exemple 3/4 = 0,75 = 0,750000000... = 0,74999999...