Enlacement - Définition

L'enlacement est un nombre entier défini pour deux courbes fermées de l'espace sans point double. Il décrit la façon dont ces deux courbes sont enlacées, liées l'une par rapport à l'autre. Il fut défini pour la première fois par Gauss.

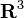
Si on peut séparer les deux courbes en les déformant sans les couper, alors l'enlacement des deux courbes vaut zéro. La réciproque est fausse.

Calcul de l'enlacement

Il existe plusieurs façons de calculer l'enlacement de deux courbes et . La plus simple consiste à projeter les deux courbes sur un plan en conservant en mémoire à chaque croisement les positions relatives des deux brins (on obtient alors un diagramme de lien. On donne à chaque courbe une orientation (sens de parcours) arbitraire et on considère les caroisement d'une courbe avec l'autre, en oubliant les éventuels croisements d'une courbe avec elle-même. On affecte à chaque croisement un indice comme défini ci-dessous (seules ces deux situations sont possibles) :

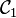
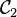
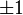
+ 1		− 1

Et on définit alors l'enlacement comme la demi-somme des indices de tous les croisement de avec .

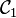
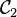
Si on change l'orientation d'une courbe, le signe de l'enlacement est changé.

Gauss a également montré qu'on peut calculer l'enlacement des deux courbes à partir d'une paramétrisation. Les points de sont parcourus par la fonction lorsque s parcourt [0,L_i], avec . On a alors la formule

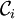
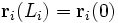
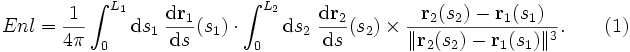
Cette formule se calcule par exemple en considérant que l'une des courbes délimite une surface et que l'autre est parcourue par un courant électrique. On obtient alors le résultat (1) à l'aide des lois de l'électromagnétisme, en calculant le courant passant à travers la surface.

Enlacement d'un ruban

On peut parler de l'enlacement d'un ruban fermé en considérant les deux bords du ruban comme courbes. Dans ce cas, l'enlacement du ruban peut se décomposer en deux termes : l'entortillement de son axe Ent et sa torsade Tor. Le théorème de C?lug?reanu-Pohl-White affirme que

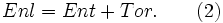
Application en biologie

L'enlacement a été utilisée pour caractériser l'enroulement des deux brins de l'ADN. Le théorème (2) est utilisé pour caractériser l'influence des déformations géométriques de l'ADN sur le surenroulement.