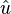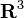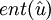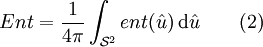Entortillement - Définition

L'entortillement est une caractéristique d'une courbe fermée sans point double dans l'espace . On peut aussi utiliser le terme vrille. Comme son nom l'indique, ce nombre décrit à quel point la courbe est entortillée, c'est à dire le degré de complexité de son chemin dans l'espace.

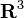
Formule générale

L'entortillement d'une courbe de longueur L et dont les points sont repérés par , avec s variant de 0 à L et s'obtient par la formule

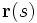
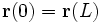
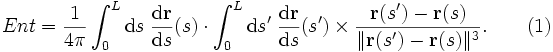
Cas d'une courbe aplatie

L'entortillement décrit la déformation de la courbe par rapport au cercle ou au nœud obtenu en aplatissant la courbe. Ainsi un cercle plat a pour entortillement zéro. Une courbe plate est représentée par un diagramme de lien, où à chaque croisement le brin passant dessous est coupé juste autour du brin passant dessus pout garder en mémoire les positions relatives, comme sur le dessin ci-dessous. On choisit arbitrairement une orientation, c'est-à-dire un sens de parcours du diagramme obtenu (ce choix ne change pas les résultats). À partir de cette orientation on obtient l'entortillement d'une courbe aplatie, qui est un nombre entier, à l'aide de son diagramme. L'entortillement est calculé en ajoutant, pour chaque croisement, + 1 ou − 1 selon la règle

+ 1		− 1

Le résultat est indépendant de l'orientation choisie pour la courbe. C'est le résultat qu'on obtient en calculant la formule (1) lorsque la courbe est aplatie.

Autre formule

La définition de l'entortillement d'un lien permet d'exprimer une formule équivalente à la formule (1). On note un vecteur unitaire de et on projette la courbe parallèlement à cette direction sur un plan. On calcule alors l'entortillement directionel en procédant comme au paragraphe précédent avec le diagramme obtenu. L'entortillement de la courbe tridimensionelle est la moyenne selon toutes les directions de l'espace de l'entortillement directionnel^[1].