Ensemble-produit - Définition
Le produit de deux ensembles est l'ensemble des couples dont le premier élément appartient au premier ensemble, et le deuxième élément appartient au deuxième ensemble.
Le produit de deux ensembles A et B se note A×B.
On peut évidemment étendre cette notion à un nombre quelconque d'ensembles :
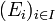
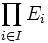
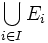
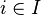
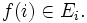
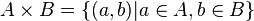
![\prod_{i=1}^n A_i = \{(a_i)_{i=1}^n|\forall i, i \in [1;n] \cap \mathbb{N} : a_i \in A_i \}](https://static.techno-science.net/illustrationWebp/Definitions/autres/6/65697c61d455bd4f856adf4abc63796c_490f9998891619234fedcbcfa47facfc.png)
Le cardinal d'un produit d'ensembles est égal au produit (dans N) de leurs cardinaux.
L'ensemble-produit est aussi appelé produit cartésien.
Plus généralement, le produit d'une famille
