Formule de Massieu - Définition
Formule de Massieu
Formule importante en mathématiques / physique établie par François Jacques Dominique Massieu
Première fonction de Massieu:
Transformation de Legendre de S(E,V,N) par E.
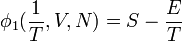
Deuxième fonction de Massieu:
Transformation de Legendre de S(E,V,N) par E et V .
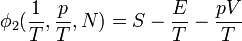
Troisième fonction de Massieu:
Transformation de Legendre de S(E,V,N) par E et N .
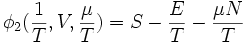
- S Entropie.
- T Température.
- V Volume.
- P Pression.
- N Nombre de particules.
- μ Potentiel chimique.

















































