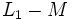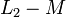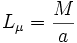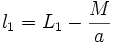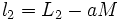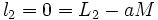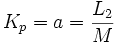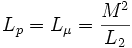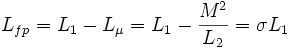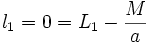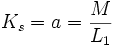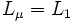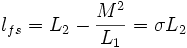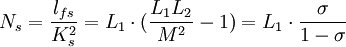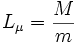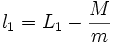Des circuits magnétiquements couplés sont des circuits électriques bobinés autour d'un même circuit magnétique. Par exemple deux enroulement d'un transformateur ou d'une machine électrique. On abrège souvent l'expression en Circuits couplés

Paramètres d'un ensemble de deux circuits magnétiquement couplés

Équations et schémas

On représente en général deux bobines magnétiquement couplées à l'aide du montage suivant :

avec et les inductances propres de chacune des bobines et  : l'inductance mutuelle.

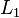
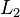
Cette modélisation occulte totalement les non-linéarités, mais elle permet de faire une étude analytique approchée (et souvent suffisante) de nombreux dispositifs de l'électrotechnique, tel que les machines électriques et les transformateurs. Les résistances des bobines ne sont pas non plus représentées, car elles ne modifient pas les démonstrations ci dessous.

Pour des raisons pratiques et/ou historiques, c'est le montage ci-dessous qui est utilisé :

Ce deuxième montage ne fait plus apparaître l'inductance mutuelle et il comporte 4 paramètres au lieu de 3. Conventionnellement le circuit d'indice 1 est appellé circuit primaire et celui d'indice 2 circuit secondaire, en référence aux tranformateurs.

• et sont appelées inductances de fuite primaire et secondaire
• est l'inductance de magnétisation ramenée au primaire.
• est le rapport de tranformation du transformateur idéal introduit dans cette modélisation.

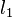
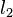
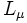
Nous verrons ci-dessous que l'un de ces paramètres est toujours choisi arbitrairement.

Une analyse mathématique des deux montages permet de montrer qu'ils sont totalement équivalents si les relations suivantes sont vérifiées :

Modèles usuels des circuits couplés

Modèle à fuites totalisées au primaire

Dans ce modèle on affirme que les fuites magnétiques n'existent pas pour l'enroulement secondaire. Le paramètre choisi est :

Ceci a pour conséquence que les paramètres de ce modèle sont liés avec les inductances par les relations :

avec :  : coefficient de fuite ou coefficient de Blondel.

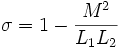
Ce modèle est particulièrement intéressant lorsqu'on s'intéresse aux effets de s inductances de fuite du circuit couplé sur l'alimentation du montage. Par exemple pour le dimensionnement du transformateur dans les alimentations à découpage de type fly-back.

Modèle à fuites totalisées au secondaire

Dans ce modèle on affirme que les fuites magnétiques n'existent pas pour l'enroulement primaire. Le paramètre choisi est :

Ceci a pour conséquence que les paramètres de ce modèle sont liés avec les inductances par les relations :

Pour des raisons de commodité, il est fréquent de ramener l'impédance de fuite du coté primaire :

Avec :  : impédance ramenée au primaire de l'inductance de fuite secondaire . Cette impédance ramenée ne doit pâs être confondue avec l'impédance de fuite primaire du précédent modèle.

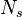
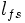
Ce modèle est très pratique pour calculer l'influence du circuit magnétique sur l'alimentation électrique quand celle-ci alimente le primaire. On l'utilise par exemple pour modéliser la machine asynchrone

Modèle à fuites séparées

Ce modèle est couramment utilisé pour les transformateurs.

On pose égal au rapport du nombre de spires de la bobine 2 par le nombre de spires de la bobine 1.

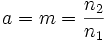
On obtient :

On peut également ramener l'inductance de magnétisation au secondaire et obtenir le modèle équivalent suivant :

avec  :

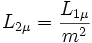
Modèle en T

On pose ce qui revient à faire disparaître le tranformateur du modèle :

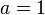
Attention ! : Ce modèle fonctionne parfaitement d'un point de vue mathématique mais il est parfois illusoire de vouloir trouver un sens physique aux trois dipôles qui le constitue.

Par exemple les valeurs de ou de peuvent être négatives, ce qui revient à dire, en régime sinusoïdal de courant, que l'inductance se comporte comme un condensateur !