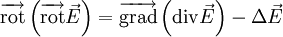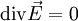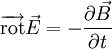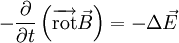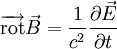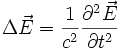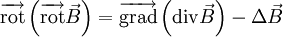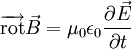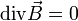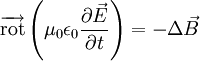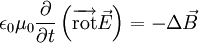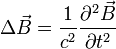Établissement de l'équation de propagation à partir des équations de Maxwell - Définition
L'équation de propagation d'une onde électromagnétique peut se calculer à partir des équations de Maxwell.
Pour le champ E
On part de la relation :
dans le vide, la charge volumique étant nulle, l'équation de Maxwell-Gauss s'écrit :
et avec Maxwell-Faraday
la relation initiale devient :
Grâce au théorème de Schwarz on peut permuter les opérateurs spatiaux et temporels et on a :
or le vecteur densité de courant
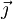
d'où :
Pour le champ B
On part de la relation :
dans le vide, la densité de courant étant nulle, l'équation de Maxwell-Ampère s'écrit :
soit :
La relation initiale devient alors :
Grâce au théorème de Schwarz on peut permuter les opérateurs spatiaux et temporels et on a :
On peut alors utiliser l'équation de Maxwell-Faraday :
On obtient alors à partir de la relation initiale, avec la relation ε0μ0c2 = 1 :