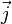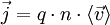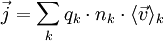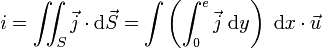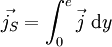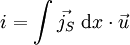Vecteur densité de courant - Définition

On notant i le courant électrique dans une portion de conducteur, et soit un vecteur élément de surface d'une section droite de ce conducteur, on pose  :

le vecteur densité de courant

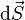
tel que

.

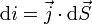
On a alors

.

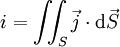
Le signe de i est alors lié à l'orientation de la surface S.

Expression de j

On montre, du fait que , que dans le cas où il n'y a qu'un seul type de porteur (électron par exemple) on a :

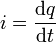
où

• q est la charge d'un porteur,
• n la densité volume des porteurs (nombre de porteurs par unité de volume) et
• le vecteur vitesse moyen des porteurs.

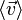
Dans le cas où il y a plusieurs types de porteurs (solution électrolytique par exemple) on aura :

A noter que dépend des autres porteurs de charges.

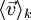
Vecteur densité de courant surfacique j_S

Supposons qu'une dimension du conducteur soit faible devant les autres, on aura alors une " feuille " d'épaisseur e négligeable, alors :

on pose alors :

ce qui donne