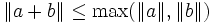Norme ultramétrique - Définition
En mathématiques, une norme ultramétrique, aussi appelée non-archimédienne est une norme (sur un K-espace vectoriel où le corps de base K est lui-même muni d'une valeur absolue ultramétrique) qui vérifie une condition plus forte que l'inégalité triangulaire, à savoir :
Cette condition se généralise aisément par récurrence, pour affirmer que la norme d'une somme est majorée par le maximum des normes des termes.
Cette condition plus forte rend vrais un certain nombre de résultats qui ne sont pas valides dans le cadre général, notamment :