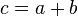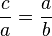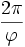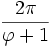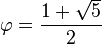Angle d'or - Définition
En géométrie, l'angle d'or est créé en divisant la circonférence c d'un cercle en 2 sections a et b( et L'angle formé par l'arc de cercle b est appelé l'angle d'or. Il mesure approximativement 137.51° ou 2.4000 radians. Il dérive du nombre d'or (φ). La mesure exacte en radians est :
On est censé retrouver cet angle à plusieurs reprises dans la nature. L'exemple le plus frappant serait la pomme de pin, sur laquelle sont présentes des spirales d'Archimède dont les points de croisement sont disposés suivant l'angle d'or.